Dark mode

الگوریتم بک‌ترکینگ در هوش مصنوعی

چکیده

توی این مقاله به تفصیل راجع به یک الگوریتم پایه‌ای توی هوش مصنوعی به نام بک‌ترکینگ یا بک‌تریسینگ حرف میزنیم و سوالات زیر رو پاسخ میدیم:

مساله n-رخ چیست؟
مساله n-وزیر چیست؟
الگوریتم بک‌ترکینگ چیست؟
مساله n-رخ با روش بک‌ترکینگ چجوری حل میشه؟
مساله n-وزیر با روش بک‌ترکینگ چجوری حل میشه؟
چجوری آرایه رو بصورت درخت در php چاپ کنیم؟

مساله nرخ و nوزیر

یکی از اهداف پایه‌ای در هوش مصنوعی این هست که ما مسائلمون رو با ریاضیات مدل کنیم و با یک الگوریتم مناسب حلشون کنیم. بک‌ترکینگ به نوع خاصی از الگوریتمها اتلاق میشه که توی اون با رفتن و برگشتن (عقبگرد کردن) میتونیم پاسخهای یه مساله ریاضیاتی رو پیدا کنیم، برای توضیح دادن این مفهوم من از دو مثال مرسوم استفاده میکنم.

دو سؤال مطرح میکنم :

سوال1:
درجه سختی: متوسط مایل به سخت

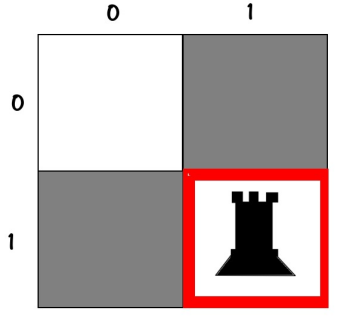
میخوایم n تا رخ رو توی یک صفحه شطرنج n×n بچینیم به شکلی که به هم گارد نگیرن، یعنی هیچکدومشون نتونن همدیگه رو بزنن؛ با توجه به هر ورودی n ؛ تمام حالتشو به صورت ماتریسی چاپ کنید...

برای n = 1 : باید یک حالت چاپ بشه:

برای n = 2 : باید ۲ حالت چاپ بشه:

برای n = 3 : باید ۶ حالت چاپ بشه:

نکته۱: صفحه شطرنجمونو به هیبت ماتریس های دودویی مربعی نشون میدیم که 1 ها نشانگر رخ ها هستن و 0 ها خونه های خالی؛

نکته۲: میدونید دیگه رخ میتونه فقط در سطر و ستون حرکت کنه و گارد بگیره.

و سؤال دوم که نسخه خفنتری از سؤال اول هستش:

سوال2:
درجه سختی: متوسط مایل به سخت

میخوام مثال مساله nرخ رو تعمیمش بدم یه یه معمای بهتر و جامع تر.

میخوایم n تا وزیر (ملکه - ملکه رو ترجمه کردن وزیر😐 ) رو توی یک صفحه شطرنج n×n بچینیم به شکلی که به هم گارد نگیرن، یعنی هیچکدومشون نتونن همدیگه رو بزنن؛ با توجه به هر ورودی n ؛ تمام حالتشو به صورت ماتریسی چاپ کنید...

برای n = 1 : باید یک حالت چاپ بشه:

برای n = 2 : نباید هیچ حالتی چاپ بشه !

مساله به ازای n=2 جواب نداره

برای n = 3 : نباید هیچ حالتی چاپ بشه !!

مساله به ازای n=3 هم جواب نداره مساله

برای n = 4 : باید دو حالت چاپ بشه:

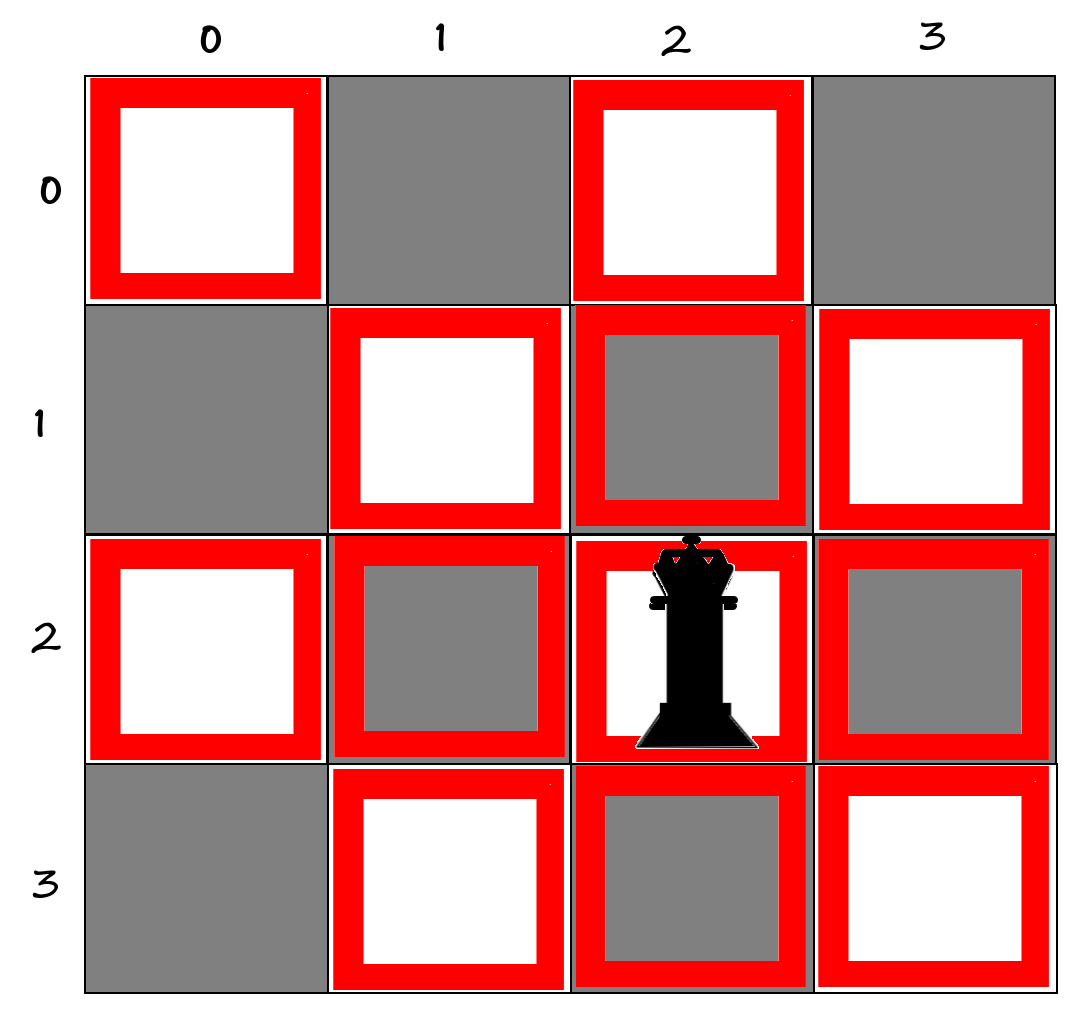
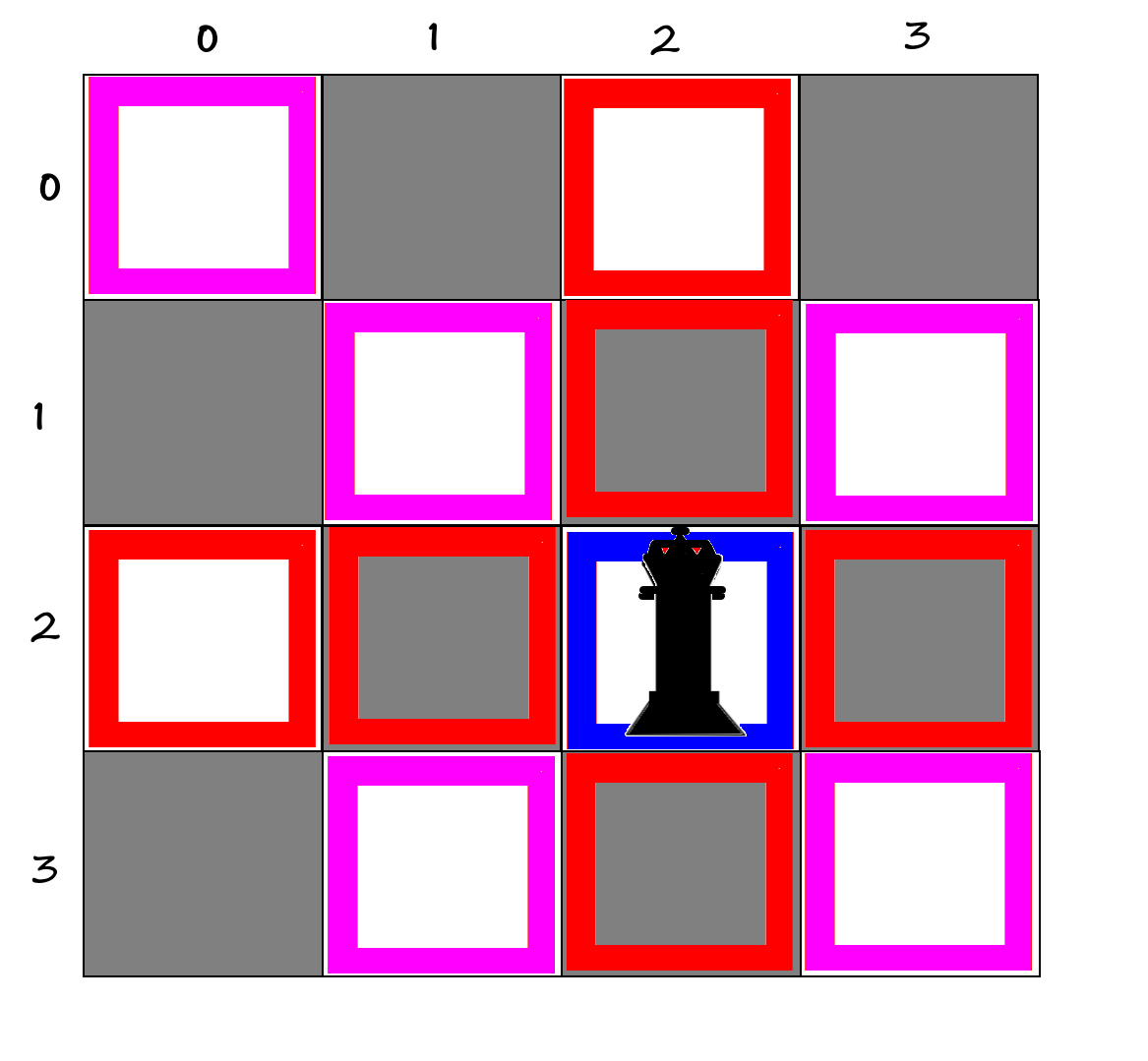
برای n = 5 : باید 10 حالت چاپ بشه:

و عکسش این 10 حالت برلی درک بهتر:

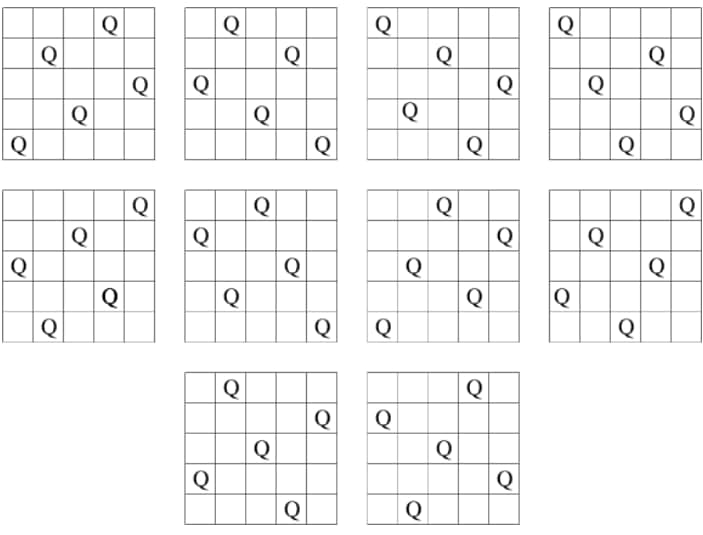
5 Queens

منبع عکس رو یادم نمیاد.

نکته۱: صفحه شطرنجمونو به هیبت ماتریس های دودویی مربعی نشون میدیم که 1 ها نشانگر وزیر ها هستن و 0 ها خونه های خالی؛

نکته۲: میدونید دیگه وزیر میتونه هم در سطر و هم در ستون و هم در قطر حرکت کنه و گارد بگیره.

الگوریتم بک‌ترکینگ چیست؟

خب حالا وقتش هست که به این سؤالهایی که مطرح کردیم پاسخ داده بشه.
قبلش چند تا مفهوم لازم رو توضیح میدم:

مساله n وزیر از مسائلی هست که نسبتاً برای ریاضی‌دان ها چالش بر انگیز بوده و همیشه دنبال حلش بصورت یک راه حل بهینه بودن ، از اونجایی که مساله‌ش برای کسانی که تازه وارد راه شدن کمی گیج‌کننده بود، تصمیم گرفتم از یک مساله ساده‌تر که مساله مساله nرخ باشه شروع کنم. چون یک ورژن ساده شده از همین n وزیر هست. یادتون باشه برنامه نویسها و الگوریتم نویسها بیشتر روی n وزیر مانور دادن.

اساتید این مساله رو به همراه یکسری مسائل ساده دیگر ، وجه ارتباط بین علم الگوریتم و علم هوش مصنوع قرار دادن ، تا الگوریتمهای هوش مصنوعی رو جهت یادگیری روی این‌ها توضیح بدن.

برای حل مساله n وزیر و ایضاً مساله nرخ ، بینهایت راه‌حل وجود داره. مثل راه حل‌های زیر که از علم الگوریتم و هوش مصنوعی استخراج شدن و راه‌حل های ریاضیاتی و ماتریسی بهمراه راه‌حل هایی که هنوز کشف نشدن...

الگوریتم عقبگرد یا Backtracking
- الگوریتم مونت کارلو
الگوریتم ارضای محدودیت یا CSP
الگوریتم مکاشفه ای یا Heuristic
الگوریتم تپه نوردی یا Hill Climbing
الگوریتم جستجوی محلی Local search
الگوریتم ژنتیک یا Genetic
و الگوریتمهای دیگری که زبان من از نام بردنشون الکن هست…

هدفی که من اینجا دنبال میکنم ، حل کردن این مساله با استفاده از الگوریتم عقبگرد یا بک‌ترکینگ هستش.

2 دلیل داره که چرا این روش (عقبگرد) رو انتخاب کردم :

استفاده این روش از درخت تصمیم یا دسیژن‌تری هستش . این روش از مدلسازی درختی استفاده میکنه ، و همین بهانه‌ای میشه که بتونم بهتون درختهارو تا حدی معرفی کنم.

این روش بر مبنای اولین راه‌حلی که به ذهن همه انسان‌ها میاد یعنی «آزمون و خطا» پیاده شده.

چرا درختها توی علم کامپیوتر اهمیت زیادی دارن؟

قبل از اینکه بخوام برم سراغ الگوریتم عقبگرد ، میخوام اهمیت درختهارو بهتون نشون بدم:

درختها عناصر جداناپذیری از علم کامپیوتر هستند، مبحث درخت خیلی خیلی خیلی خیلی خیلی مبحث مهمی هست… تمــــــااام کسایی که وارد عرصه کامپیوتر میشن دیر یا زود به یادگیری درختها نیاز پیدا میکنن.

بسیاری از فرمتهای هارددیسک برای پیکربندی پارتیشنها فایلها از درخت استفاده میکنن.
مثلاً فرمت ext از چیزی به اسم inode استفاده میکنه که در‌واقع همون درخت هست.
ذخیره سازی فایلها! ذخیره سازی فایلها و پیکربندی دایرکتوری ها ، در همه دنیا با یک درخت مدل شده. دایرکتوری اصلی ، دایکتوری روت (ریشه) هستش و بقیه دایرکتوری های فرزندانش میشن… و هر کدوم فرزندانی دارن و … اگه باورتون نمیشه، دستور tree رو بزنید تا ببینید.
تمامی پیکر بندی های دایرکتوری در لینوکس یا هر سیستم عامل دیگه با یک درخت انجام گرفته (حتماً شنیدید که میگن دایرکتوری parent - یعنی نود پدر در درخت)
سریعترین – تأکید میکنم – سریعرتین دیتابیسهای دنیا بر پایه درخت نوشته شدن. مثال میزنم:
دیتابیس مای‌سیکوئل بر پایه درخت B نوشته شده.
دیتابیس مونگو بر پایه درخت +B (بی پلاس) نوشته شده.
وقتی ما اطلاعات رو توی یک درخت خود متوازن مثل بی‌پلاس ذخیره میکنیم ، سرعت دسترسی/جستجو/خوندن/نوشتن بطور عجیبی بالا میره ، با استفاده از فرمولهای ریاضی ثابت میشه که در بدترین حالت با یک جستجوری لگاریتمی مساله حل میشه ، مثلاً توی 1 ملیارد دیتای ذخیره شده ، با کمتر از 20 بار مقایسه و سیک کردن ، دیتا رو پیدا میکنیم! (فکر کردین اینستاگرام چه‌جوری بین ملیاردها پست و کاربر سوییچینگ رو انجام میده ؟! )
تمام سوشال مدیا و شبکه‌های اجتماعی بر پایه گراف (شکل کلی تری از درخت) نوشته شدن ،… تمامشون : تلگرام – اینستا – فیسبوک - ….
سرچ‌انجین ها برای ذخیره داکیومنتهای ایندکس شده از درختها استفاده میکنن.
سیستم عامل افسانه‌ای یونیکس بر پایه درخت است
به تبع قسمت قبلی، کل لینوکس بر پایه درخت نوشته شده – کُلّش
دسترسی یوزر های توی لینوکس با درخت مدل شده (دسترسی روت شنیدین دیگه،‌ روت یعنی ریشه درخت)
هندل کردن تمــــامی پراسس های سیستم عامل توی یه سیستم مبتنی بر یونیکس مثل لینوکس بر پایه درخت نوشته شده. باورتون نمیشه ؟ دستور pstree رو بزنید تا درخت پراسس سیستم عاملتون رو ببینید.
هندل کردن تمامی نخ های سیستم عاملها بر پایه درخت صورت گرفته.
امرزوه 90 درصد سیستم عاملهای جهان بر پایه لینوکسن ، فلذا بر پایه درخت نوشته شدن.
از بین بقیه‌شونم اونهایی که بر پایه یونیکس هستن بازم درختی هستن.
تمام عناصر شبکه با گراف مدلسازی شدن.
کسر بالایی از آرایه های داینامیک با درخت نوشته شدن
HTML بر پایه درخت طراحی شده.
HTML/XML روی درخت پارس میشه.
توی علم وب چیزی به اسم DOM وجود داره که صفحه وب رو روی یه درخت مدل میکنه
توی طراحی کامپایلرها/مفسرها و کلاً زبانهای برنامه‌نویسی درخت نقش اصلی رو بازی میکنه.
توی هوش مصنوعی درخت نقش گسترده‌ای داره، که ما یه ذره‌ش رو اینجا نشون دادیم.
بسیاری از الگوریتمهای روتینگ شبکه‌ای روی درختها کار میکنن.
ساختار سلسله مراتبی DNS ها در‌واقع روی یه درخت هست (مثلاً شنیدین DNSهای ریشه؟)
سیستمهای ورژن کنترل (VCSها) مانند git در‌واقع روی یه درخت ترک هاشون رو انجام میدن.
...

خب من دیگه از مزایای درختها چیزی نمیگم چون اگه ادامه بدم دیگه به ادامه مقاله‌مون نمیرسیم…

پس درخت چیز مهمی هست…

خب خب خب… یک راست بریم سراغ حل مساله مساله nرخ :

الگوریتم بک‌ترکینگ میفرماید که :

«سلام ، خوبی؟
میخوای یک مساله سخت ریاضی رو با من مدلسازی کنی ؟ یعنی میخوای راه حلتو تبدیل کنی به یک راه‌حل استاندارد؟؟ مساله و راه حلتو با استفاده از یک درخت مدل کن…»

حالا این یعنی چی؟

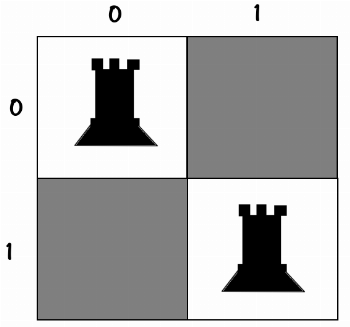
فرض کنید که به یک نفر که نا‌آشنا با علم ریاضیات و الگوریتمه میگی که بیا این 8 تا رخ رو روی این صفحه شطرنج بطوری بچین که به هم گارد نگیرن :
این حضرت شروع مکینه به چیندن ، اولی رو میذاره بعدش دومی رو میذاره … بعدش… به 5 امی که میرسه میبینه عه، اینکه گذاشتمش که میتونه سومی رو بزنه… : / هیچ جایی هم نیست که بذاریمش که گارد نگیره…
پس برمیگرده عقب و چهارمی و سومی رو جاهاشون رو تغییر میده. تا بالاخره یکی از جوابهارو پیدا کنه و بهت بده.
این جناب ناخواسته از الگوریتم عقبگرد یا بک‌ترکینگ استفاده کرده .
+++ البته : هدف ما توی این مقاله پیدا کردن اولین جواب ممکن نیست ، هدف پیدا کردن تمامی جوابهای ممکنه .
در الگوریتم بک‌ترکینگ ما یک درخت تصمیم میسازیم و مساله‌مونو روی اون درخت مدل میکنیم:
قبل از اینکه درختشو برای چندتا n اول ماجرا بهتون نشون بدم ، کلاً ساختار یک درخت رو با چندتا عکس معرفی مکینم تا اگر گفتم – نود – ریشه – پدر – فرزند – برگ – عمق - سیبلینگ … گیج نشین ، ولی نمیتونم کل درختهارو اینجا توضیح بدم…. توضیح درختها یک کتاب 100 جلدی میطلبه… شایدم بیشتر !!

درخت چیست؟ (توضیح ساده)

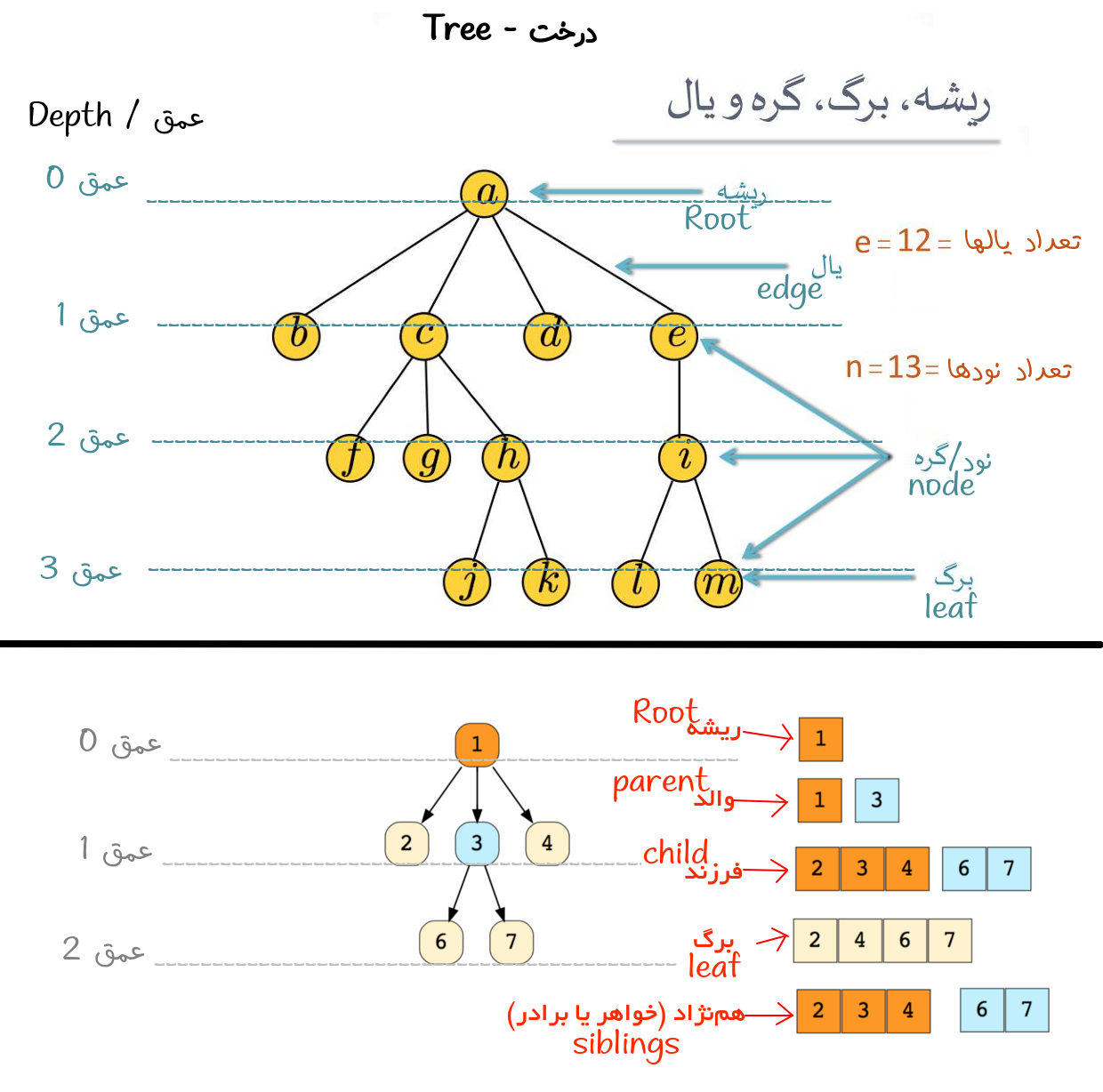
Tree structure

توضیحات :

تعریف تخصصی درخت = درخت گرافی هست که دور نداشته باشه.

درست همانند درختای توی باغ ، هر درخت حتماً فقط و تنها فقط یک ریشه داره – درختی نداریم که ریشه نداشته باشه ، حتی درختی با یک نود ، همون یک نودش ریشه میشه(البته برگ هم حساب میشه – جلوتر ببینید).
یال : تعریف یال در گراف هارو بخونین اونجا بیشتر کاربرد داره ، توی درخت یال گره هارو به هم وصل میکنه همین. چیزی خاصی نیست.
نود/گره … به اون گردی هایی که توش مقدار مینویسیم میگن نود یا گره^_^ برای تعریف تخصصی گرافهارو مطالعه کنید.
برگ : به نودی که فرزند نداشته باشه میگن برگ.
پدر/والد : نودی که فرزند داشته باشه برای فرزندهاش میشه پدر
فرزند : به نودی که مستقیما نشأت گرفته از یک نود دیگه هست ، میگن فرزند اون نوده
سیبلینگ/همنژاد : به نود هایی که از یک پدر باشن میگن خواهر برادر یا سیبلینگ
عمق : عمق تعریف تخصصی داره ، فک کنم به تعداد یالهای که پیمایش شده تا از ریشه به اون نود برسیم میگن نود ، ولی خب روی شکل نشونش دادم… راحت متوجه میشین عمق چیه دیگه...

نکته مهم : من بیشتر از این راجع به درختها توضیحی نمیدم ، برای یادگیری درختها لازمه که گرافها رو یاد بگیرید ، پس از شاخه ریاضیات گسسته ، گراف هارو مطالعه بفرمائيد.

چجوری مساله nرخ و nوزیر رو با روش بک‌ترکینگ حل کنیم؟

اوکی بیایید مساله رو با درخت با استفاده از بک ترکنیگ مدل کنیم :
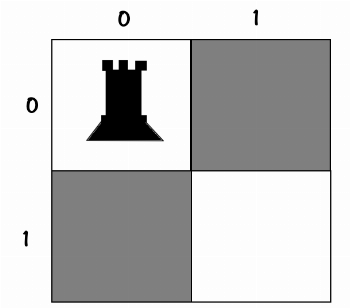
به ازای n = 1 چی داریم؟
یک صفحه شطرنج یه دونه ای:

1 chess

فلذا ساخت درختش خیلی کار سختی نیست:
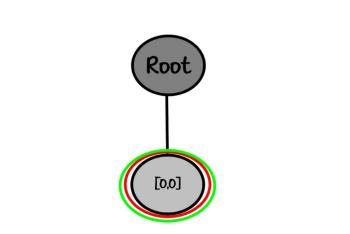
یک رخ رو میذاریم توی صفحه با مختصات [0,0] بعدش چک میکنیم که آیا اوکی هست یا نه برش داریم و برگریدم عقب ،… اوکیه ! فلذا بای‌بای ^_^

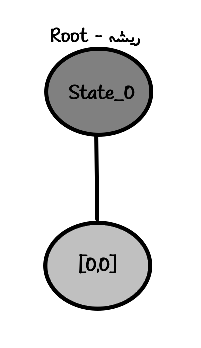
1 tree

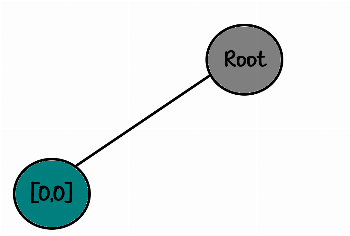
"root"
State_0
    └── [0,0]

ریشه رو ببینید چی اتخاذ کردم ، استیت 0 – یعنی S0 یعنی نقطه شروع یعنی وقتی هنوز هیچ چیزی رو پلیس نکردیم. این اختیاریه دست خودتونه … به یک هیبت دیگه بنویسیدش…

به ازای n = 2 یکم کار جذاب‌تر میشه
ببینید خشگلای من ، صفحه شطرنج و درخت تصمیم به این شکله:

2 chess

00
00

2 tree

"root"
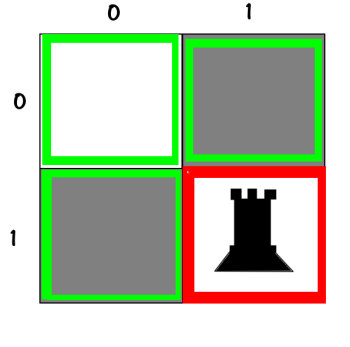
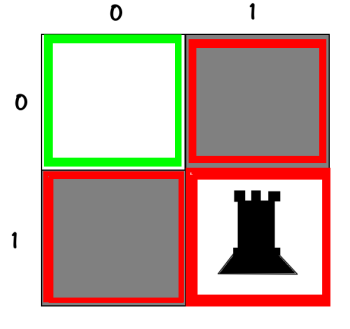
State_0

مساله خیلی خیلی مهم : توی سؤالی که از محضرتون پرسیدم ، این نکته نهفته هست که بین رخ ها یا وزیرهای متفاوت هیچ تفاوتی وجود نداره یعنی رخ اول با رخ دوم انگار که یکی هستن ، اصطلاحاً هیچ تمییزی بین اونها قائل نیستیم ، توی کدی که زدم و خدمتتون ارسال میکنم ، شما میتونید مشخص کنید که بین مهره‌ها توی حل مساله تمییز قائل بشه یا نه. الان بیشتر توضیح میدم : فرضی که ما کردیم اینه که :

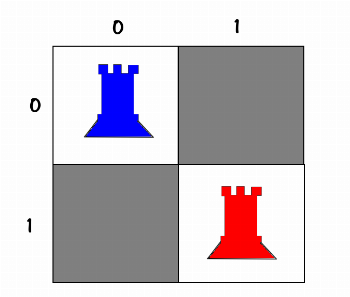
2 queens alternative

10
02

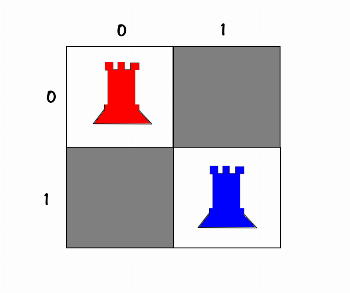
2 queens alternative

20
01

در دو حالت بالا، که توی عکس، رخ آبی مثلاً [1] اولین رخی باشه که place کردیم و قرمز [2] دومی باشه، توی سؤال فرض کردیم که هیچ تفاوتی ندارن و هر دو نمایانگر تک‌حالت زیر هستن:

2 queens alternative

10
01

و اما حالت کلی‌تر اینه که بیایم بین رخ ها تفاوت هم قائل بشیم. چون پاسخ‌های این حالت ، کامل‌تر هستن و شامل پاسخ‌های قسمت «بی‌تفاوت‌» هم میشن .

حالا بیاین با بک‌ترک حلش کنیم :
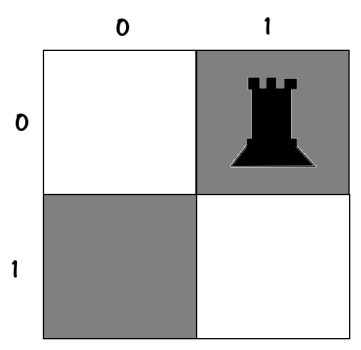
رخ اول رو بذاریم توی خونه [0,0] :

2 chees1

10
00

درخت تصمیم تا به اینجا به هیبت زیره :

2 tree1

root
└── [0,0]

خب حالا وقتشه که رخ دوم رو بذاریم : طبق ترتیب اولیش رو گذاشتیم توی [0,0] فلذا دومی رو میذاریم توی [0,1] ، فی‌الواقع داریم:

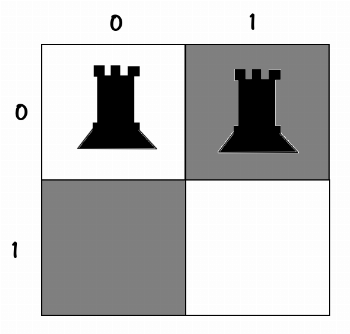
2 chess2

11
00

درخت تصمیم اینجوری میشه :

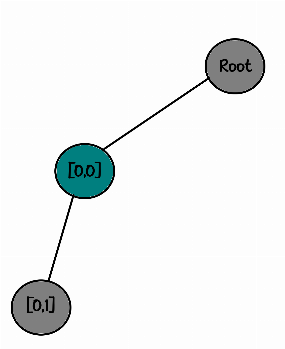
2 tree2

root
└── [0,0]
    └── [0,1]

و اما و اما …. چک میکنیم که آیا اوکیه؟ میبینیم نه اوکی نیست! رخ ها به هم گارد دارن! فلذا رد پامونو دنبال میکنیم و یک قدم برمیگردیم عقب ( اصطلاحا بک‌ترک میکنیم ) مهره ای که گذاشتیم رو بر میداریم و توی درخت به نود پدرش میریم و اون نود فرزند رو میذاریم کنار – جواب ما نبود!

2 chess1

10
00

و درخت تصمیم دوباره میشه :

2 tree1

root
└── [0,0]

اینکه من نودش رو توی شکل پاک کردم ، دلیل نمیشه توی کد زنی هم پاکش کنم،‌ بستگی به نحوه پیاده‌سازی برنامه‌نویس داره ، ممکنه بگه من نود های ویزیت شده رو - اگر جواب نباشن -میخوام نگه دارم که بعداً بفهمم اینارو ویزیت کردم… یا اینکه معماری رو جور دیگری پیاده کنه...
به هرحال بعداً درخت کاملشو میکشم ، الان درگیر این مسائل نشین .

خب طبق ترتیب رخ بعدی رو میزاریم توی خونه [1,0] فلذا داریم:

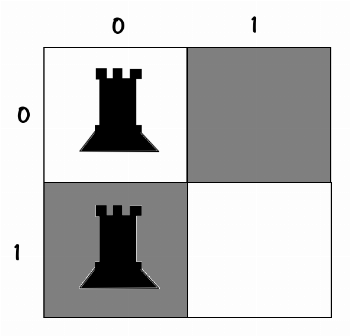
2 chess3

10
10

درخت تصمیم :

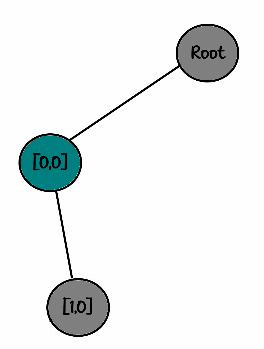
2 chess3

root
└── [0,0]
    └── [1,0]

و اما… بازم به هم گارد دارن که :(
بازم بک ترک…

2 chess1

10
00

و باز هم درخت میشه :

2 tree1

root
└── [0,0]

حالا نوبت به جای آخر میرسه رخ رو میذاریم توی خونه [1,1] :

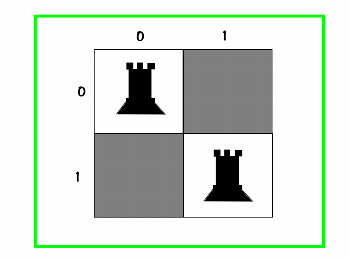
2 chess4

10
01✅

و جناب درخت تصمیم :

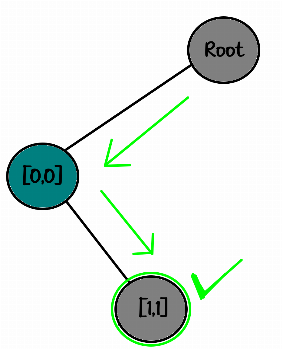
2 tree4

root
└── [0,0]
    └── [1,1]✅

چک میکنیم، این یکی از حالتهای پاسخ مساله هستش ، فلذا ووووووهووووو :)
میخوایم چاپش کنیم یا میخوایم ذخیره‌ش کنیم ، هر بلایی بخوایم سرش بیاریم ، میاریم و میریم سراغ مرحله بعدی.

بک ترک میکنیم تا موقعی که صفحه خالی میشه :

2 rooks placement

00
00

و درخت میشه :

2 tree

root

یک بار دیگه میگم! قضیه اینطوری نیست که نود هارو پاک کنیم! من چون الان دارم سلسله مراتبی توضیح میدم، چونکه شلوغ نشه و گیج نشین اینجوری نوشتم.

بگذریم

رخ اول رو سری قبلی توی [0,0] گذاشتیم ، این سری توی [0,1] میگذاریم طبق ترتیب:

2 rooks placement

01
00

و درخت :

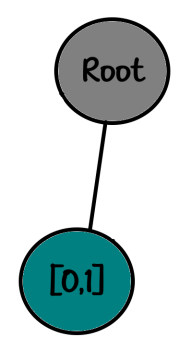
2 rooks placement

root
└── [0,1]

من دیگه مراحل رو سریع تا آخر میگم :

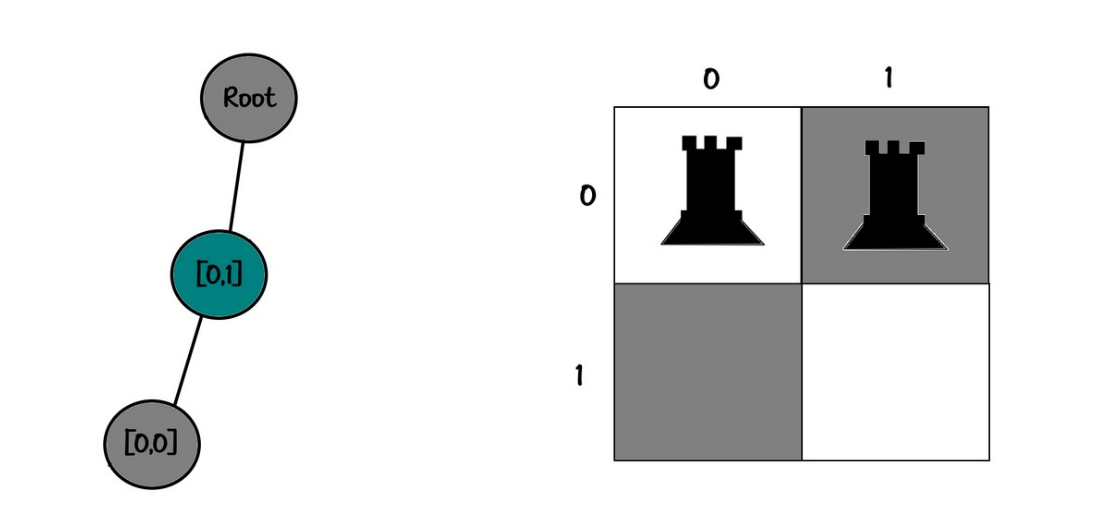
2 rooks placement

Board:
11
00

Tree:
root
└── [0,1]
    └── [0,0]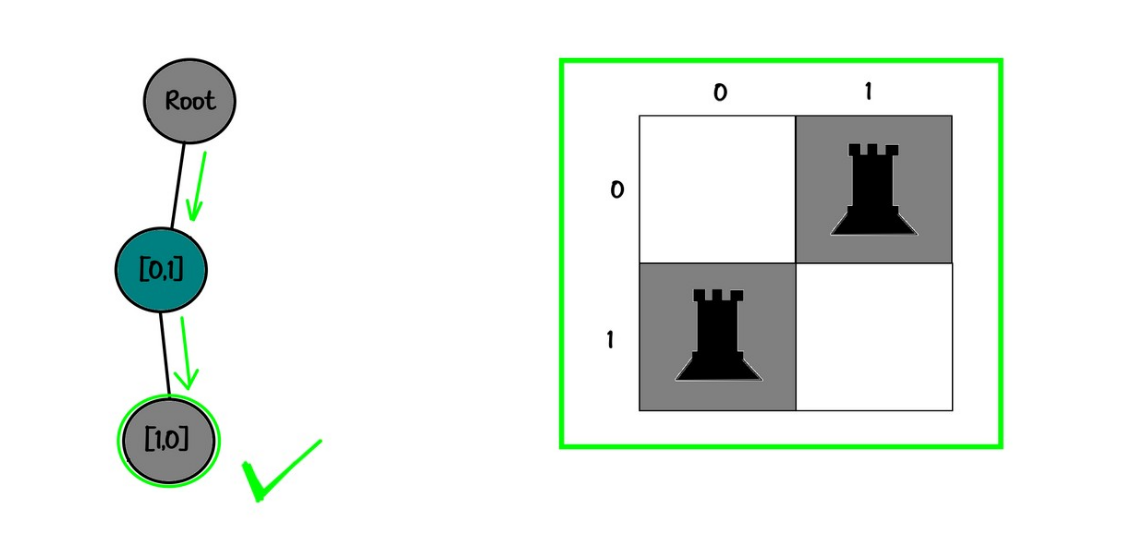

2 rooks placement

Board:
01
10✅

Tree:
root
└── [0,1]
    └── [1,0]✅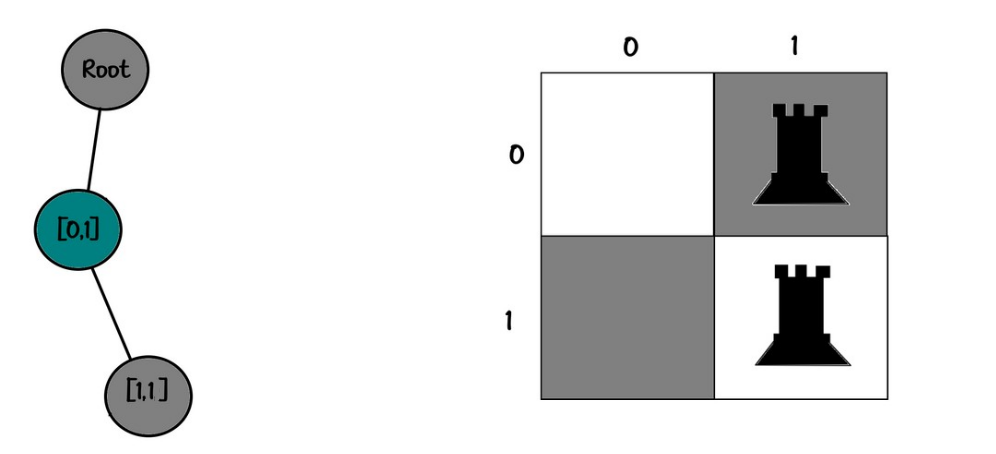

2 rooks placement

Board:
01
01

Tree:
root
└── [0,1]
    └── [1,1]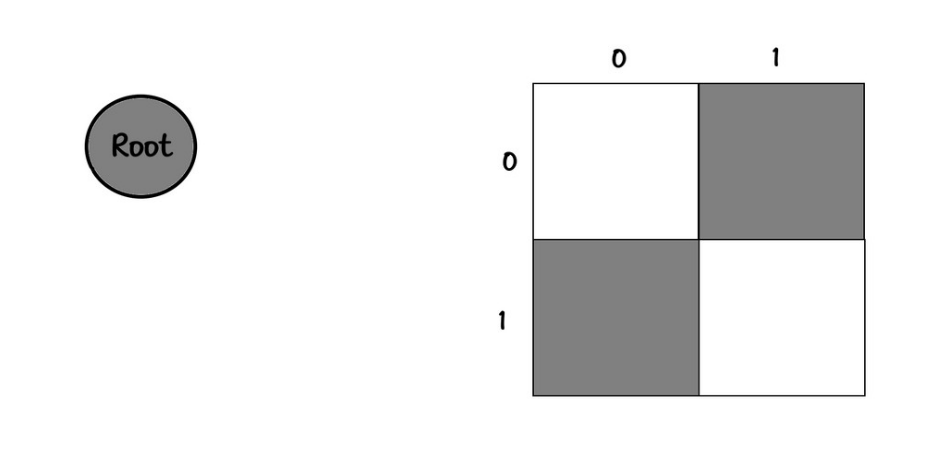

2 rooks placement

Board:
00
00

Tree:
root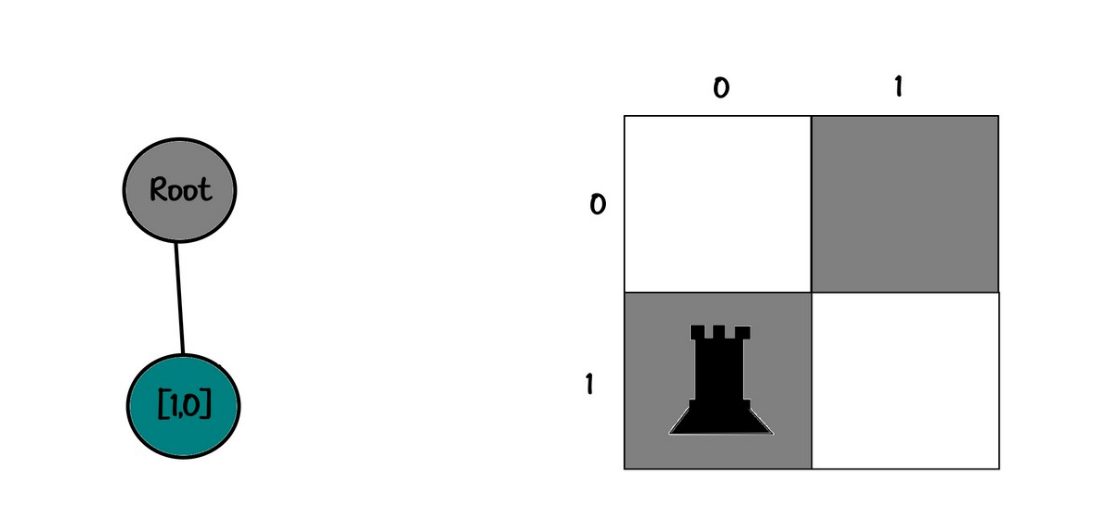

2 rooks placement

Board:
00
10

Tree:
root
└── [1,0]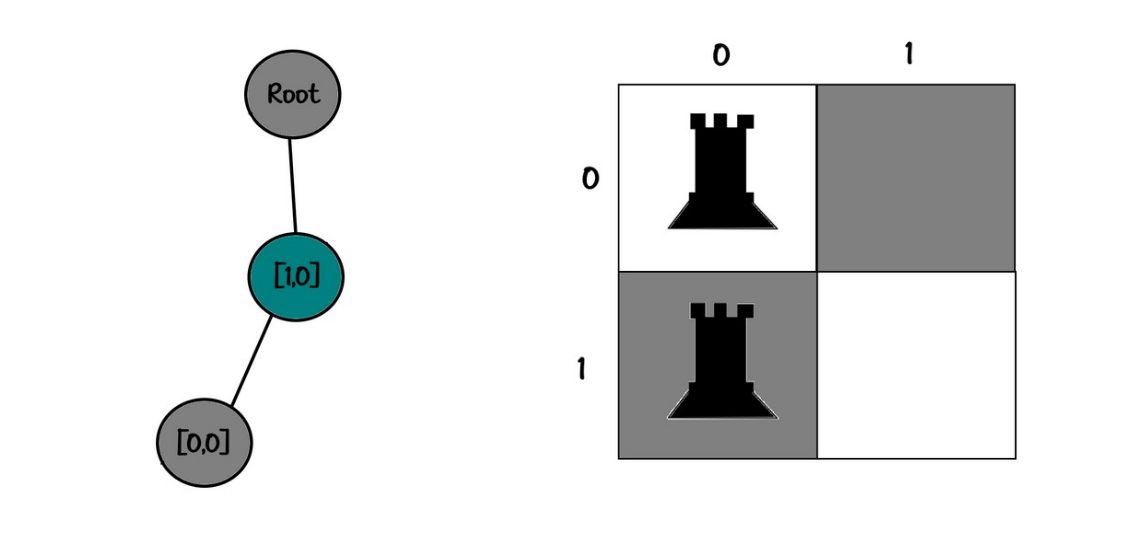

2 rooks placement

Board:
10
10

Tree:
root
└── [1,0]
    └── [0,0]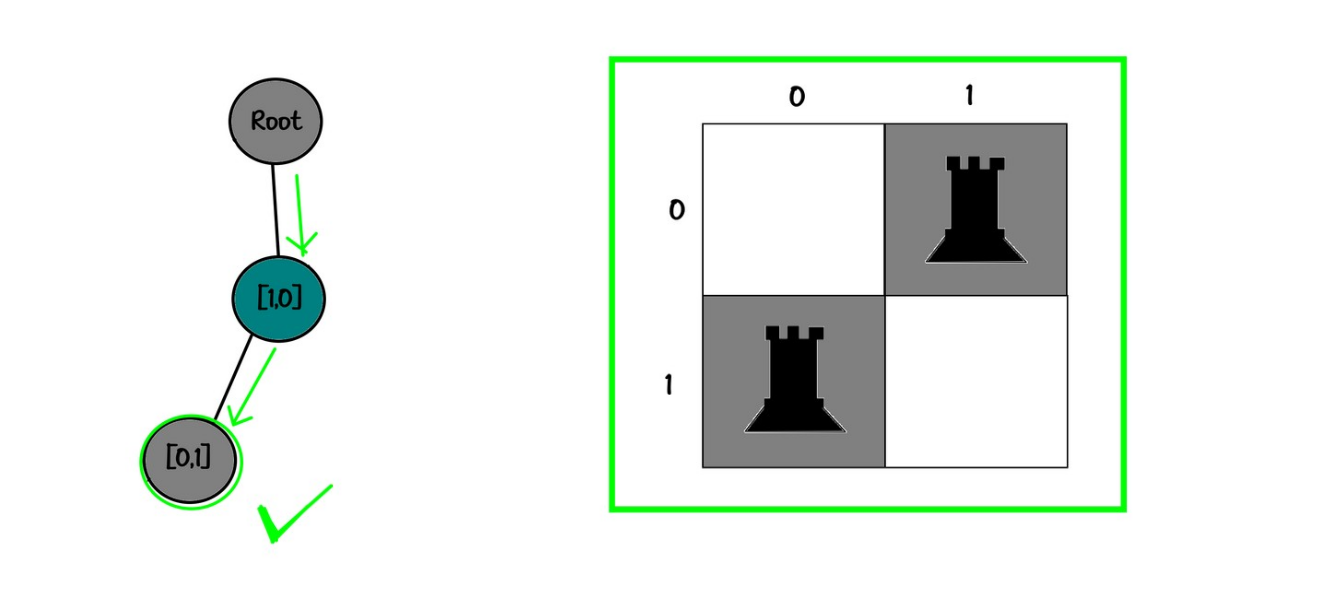

2 rooks placement

Board:
01
10✅

Tree:
root
└── [1,0]
    └── [0,1]✅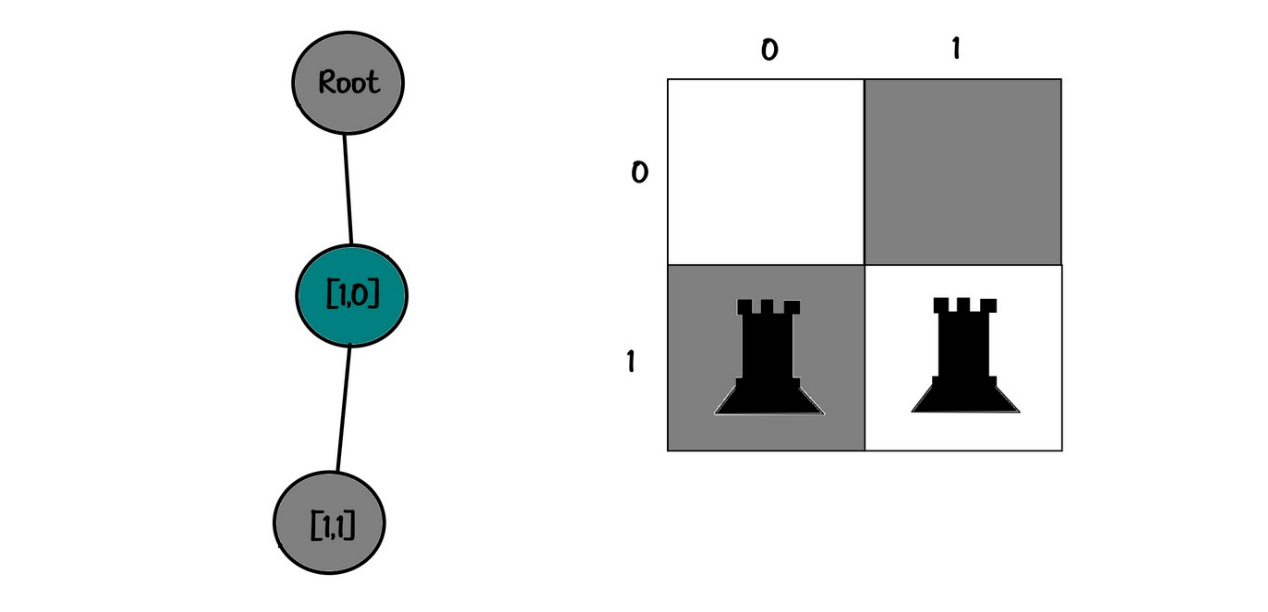

2 rooks placement

Board:
00
11

Tree:
root
└── [1,0]
    └── [1,1]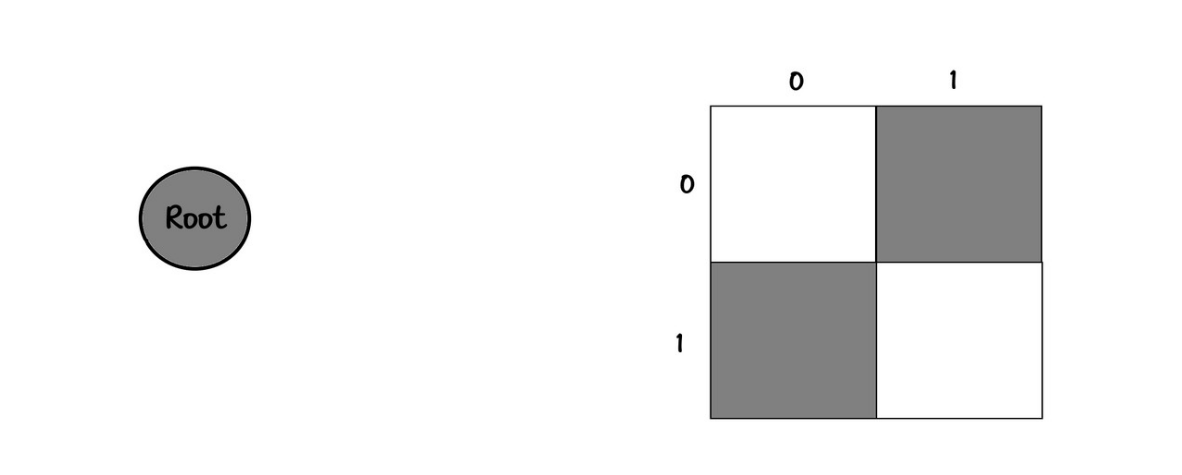

2 rooks placement

Board:
00
00

Tree:
root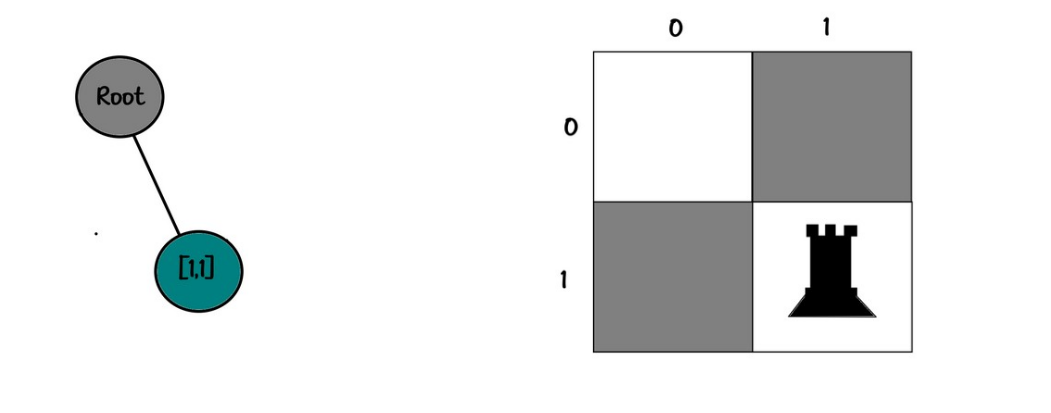

2 rooks placement

Board:
00
01

Tree:
root
└── [1,1]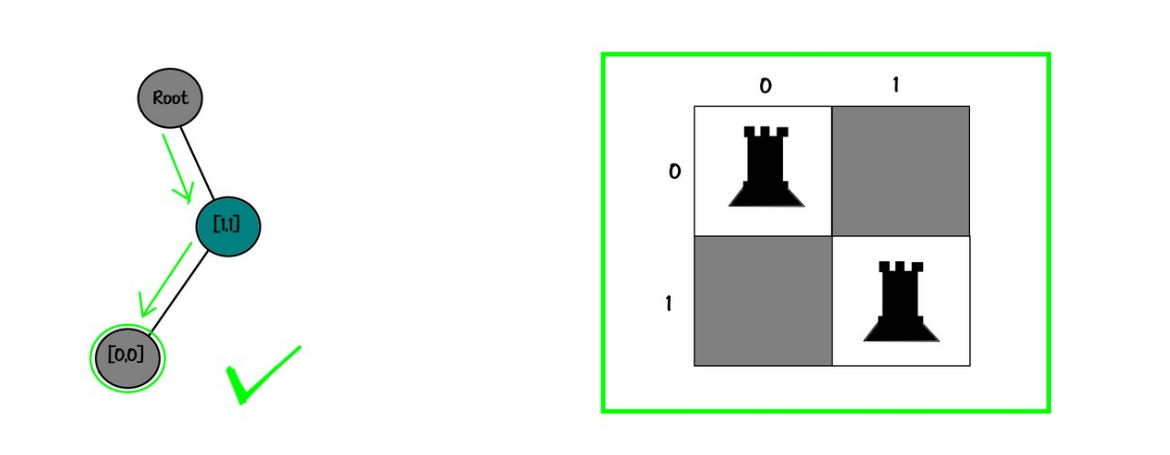

2 rooks placement

Board:
10
01✅

Tree:
root
└── [1,1]
    └── [0,0]✅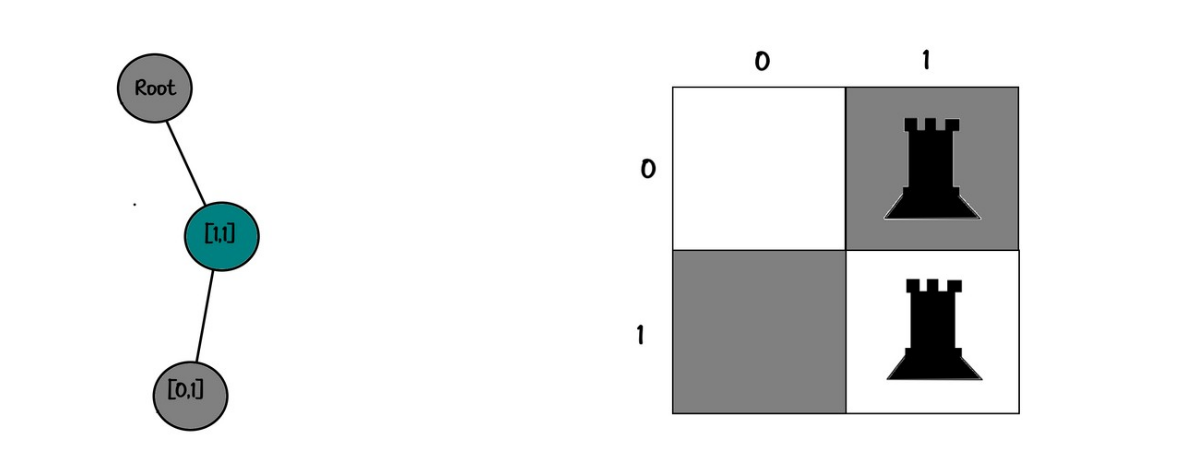

2 rooks placement

Board:
01
01

Tree:
root
└── [1,1]
    └── [0,1]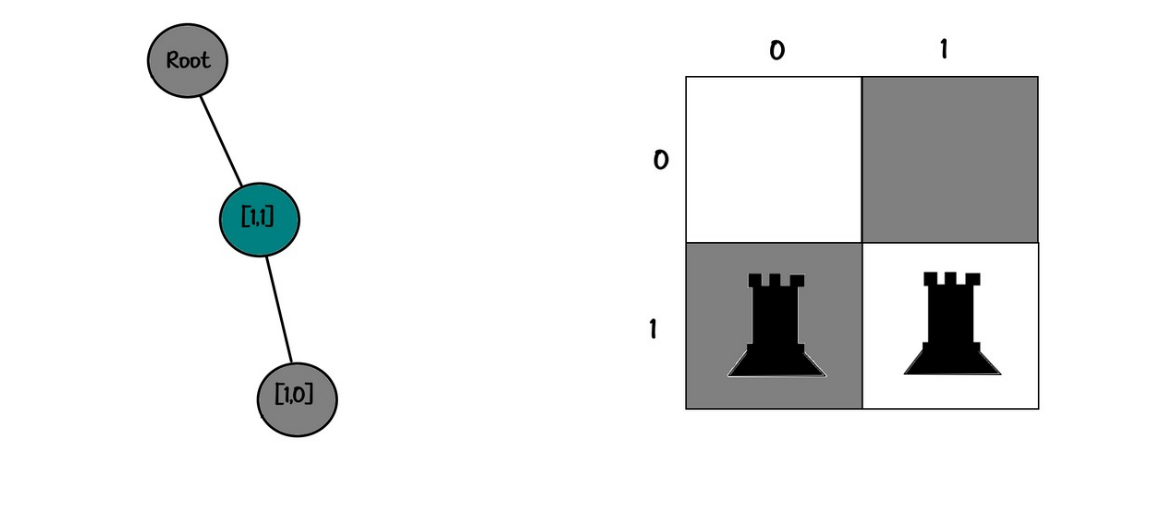

2 rooks placement

Board:
00
11

Tree:
root
└── [1,1]
    └── [1,0]

و تمااااااااااام :)
تمام جوابهای ممکن رو پیدا کردیم 4 جواب (با تفاوت) :

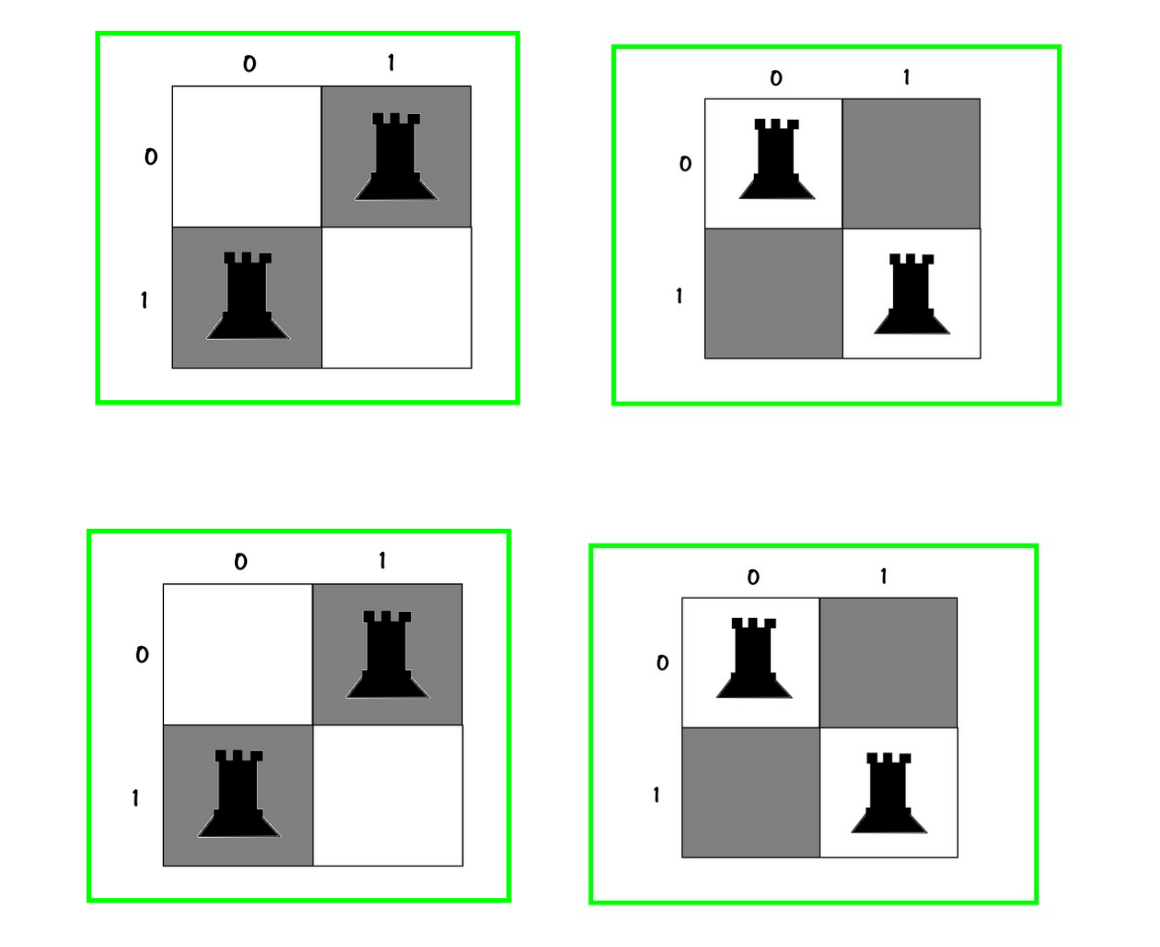
2 rooks placement

و اگر بین رخ ها تمییز قائل نشیم فقط :

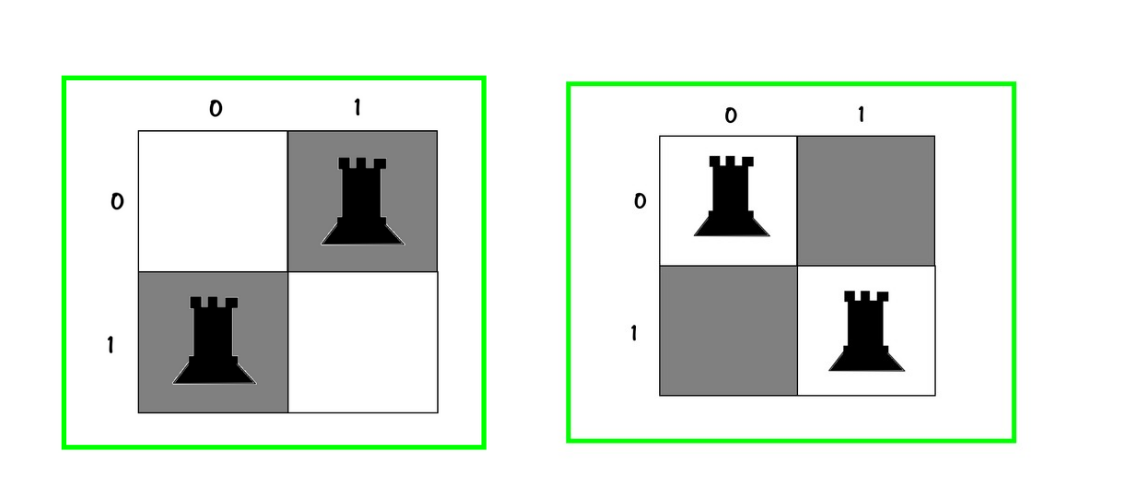
answers with no distinguish

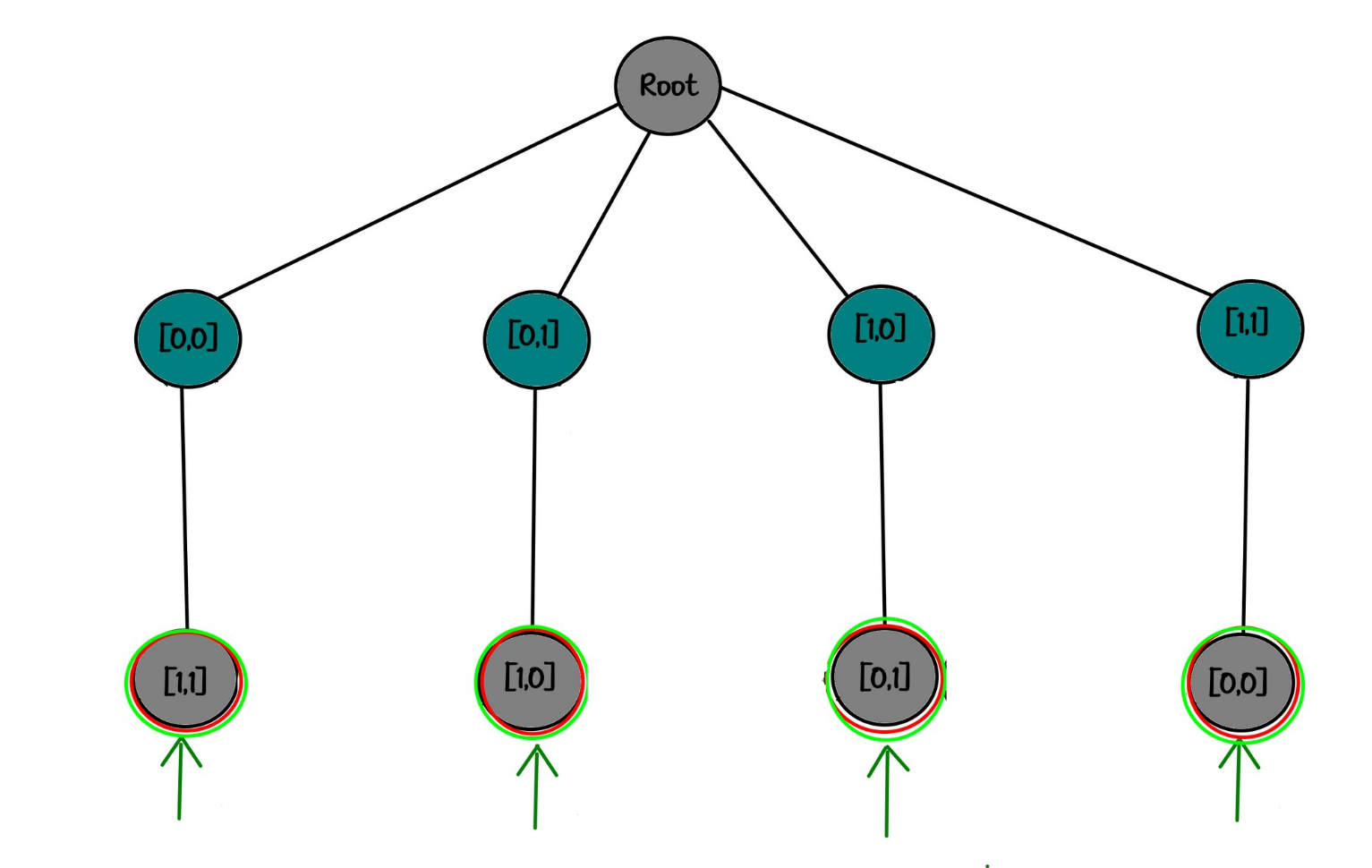
خب حالا وقتشه که درخت تصمیم واقعی که برای مساله 2 رخ باید متصور بشه ، رو ویژوآلایز کنم :
خوب درختشو نظارت کنید که خیلی مهمه!

اگر تفاوت قائل بشیم (که کامپیوتر همیشه قائل میشه و شما باید جوری تنظیم کنید که خروجیتون فیلتر بشه):
• بار اول 4 انتخاب داریم
• بار دوم 3 انتخاب (چون نمتونیم یه رخ رو بندازیم تو بغل یک رخ دیگه… از لحاظ اخلاقی… 😋)

کلاً میشه 12 حالت که دونه دونه گفتم چجوریاست.

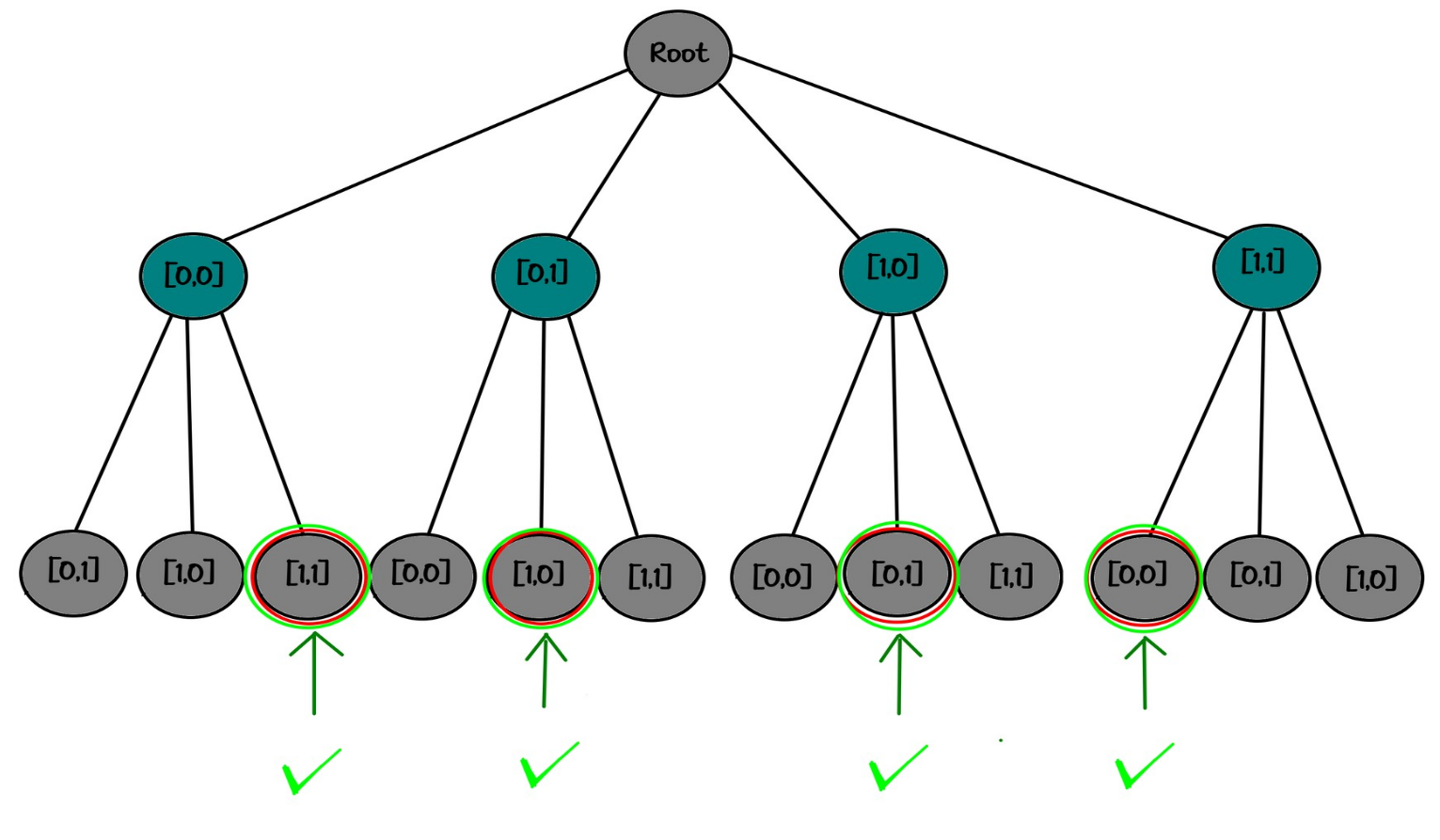
2 rooks whole tree

"root"
├── [0,0]
│   ├── [0,1]
│   ├── [1,0]
│   └── [1,1]✅
├── [0,1]
│   ├── [0,0]
│   ├── [1,0]✅
│   └── [1,1]
├── [1,0]
│   ├── [0,0]
│   ├── [0,1]✅
│   └── [1,1]
└── [1,1]
    ├── [0,0]✅
    ├── [0,1]
    └── [1,0]

خب خب خب …

این‌ام از الگوریتم بک ترکینگ و توضیح تخصصیش…
و اما…
و اما….
برنامه‌نویس باید به خیلی از موارد فکر کنه… باید همیشه بهینه ترین کد رو بزنه ، قبل تر که ما میومدیم و یک رخ رو توی یک خونه خاص میذاشتیم مثلاً :

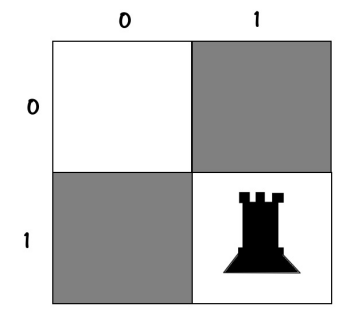
2 rooks placement

00
01

برای پلیس کردن رخ دوم ، خونه ی زیر فقط غیر مجاز بود :

2 rooks placement

00
0X

و بقیه خونه هارو مجاز میپنداشتیم ، و توش رخ میذاشتیم و تست میکردیم…

2 rooks placement

VV
VX

ولی آیا این کار درسته؟
خیــــــــــــــــــــر اصلا درست نیست!

وقتی رخ اول رو گذاشتیم اینجا :

2 rooks placement

00
01

این حضرت در راستای افق و عمود خودش گارد میتونه بگیره – فلذا :

2 rooks placement

VX
XX

دیگه چک کردن قسمت‌های قرمز رنگ (X ها) کار سخیف و بیهوده‌ایه ^_^
با این اوصاف بنده درخت تصمیم رو به این شکل تعمیمش میدم :

2 rooks tree rewised

"root"
├── [0,0]
│   └── [1,1]✅
├── [0,1]
│   └── [1,0]✅
├── [1,0]
│   └── [0,1]✅
└── [1,1]
    └── [0,0]✅

اهوم...
تموم شد و رفت :)
اگر متوجه نشدید لختی درنگ کنید و سعی کنید با این فرض محدودیت جدید خودتون درخت رو بکشید.

جا داره که یواشکی بگم انگاری پاسخ‌های مساله مساله nرخ ما (و بعداً n وزیر) همیشه در عمق n ام درخت ما قرار دارن…. هیسسسس به کسی نگینا

خب دیگه حالا با این فرض جدید ، درخت تصمیم مربوط به n های برابر با 1 و 2 و 3 رو میکشم و ازش رد میشم:
برای n = 1 داریم :

2 rooks tree

"root"
└── [0,0]✅

برای n = 2 داریم :

2 rooks tree rewised

"root"
├── [0,0]
│   └── [1,1]✅
├── [0,1]
│   └── [1,0]✅
├── [1,0]
│   └── [0,1]✅
└── [1,1]
    └── [0,0]✅

برای n = 3 داریم :
خسته شدم از بس درخت گرافیکی کشیدم... هر چند که شک دارم کسی اینارو بخونه!
بجاش با الهام گرفتن از کامند tree توی لینوکس یه تابعِ سکسی نوشتم که درخت رو تحت ترمینال ویژوآلایز میکنه:

.
└── "root"
    ├── [0,0]
    │   ├── [1,1]
    │   │   └── [2,2]
    │   ├── [1,2]
    │   │   └── [2,1]
    │   ├── [2,1]
    │   │   └── [1,2]
    │   └── [2,2]
    │       └── [1,1]
    ├── [0,1]
    │   ├── [1,0]
    │   │   └── [2,2]
    │   ├── [1,2]
    │   │   └── [2,0]
    │   ├── [2,0]
    │   │   └── [1,2]
    │   └── [2,2]
    │       └── [1,0]
    ├── [0,2]
    │   ├── [1,0]
    │   │   └── [2,1]
    │   ├── [1,1]
    │   │   └── [2,0]
    │   ├── [2,0]
    │   │   └── [1,1]
    │   └── [2,1]
    │       └── [1,0]
    ├── [1,0]
    │   ├── [0,1]
    │   │   └── [2,2]
    │   ├── [0,2]
    │   │   └── [2,1]
    │   ├── [2,1]
    │   │   └── [0,2]
    │   └── [2,2]
    │       └── [0,1]
    ├── [1,1]
    │   ├── [0,0]
    │   │   └── [2,2]
    │   ├── [0,2]
    │   │   └── [2,0]
    │   ├── [2,0]
    │   │   └── [0,2]
    │   └── [2,2]
    │       └── [0,0]
    ├── [1,2]
    │   ├── [0,0]
    │   │   └── [2,1]
    │   ├── [0,1]
    │   │   └── [2,0]
    │   ├── [2,0]
    │   │   └── [0,1]
    │   └── [2,1]
    │       └── [0,0]
    ├── [2,0]
    │   ├── [0,1]
    │   │   └── [1,2]
    │   ├── [0,2]
    │   │   └── [1,1]
    │   ├── [1,1]
    │   │   └── [0,2]
    │   └── [1,2]
    │       └── [0,1]
    ├── [2,1]
    │   ├── [0,0]
    │   │   └── [1,2]
    │   ├── [0,2]
    │   │   └── [1,0]
    │   ├── [1,0]
    │   │   └── [0,2]
    │   └── [1,2]
    │       └── [0,0]
    └── [2,2]
        ├── [0,0]
        │   └── [1,1]
        ├── [0,1]
        │   └── [1,0]
        ├── [1,0]
        │   └── [0,1]
        └── [1,1]
            └── [0,0]

و تموم:)
راستی قبل از اینکه هر کاری کنید:
نوشتن این تابع میتونه یک تمرین خوب برای تمرین قدرت برنامه نویسیتون باشه

تمرین1 : بدون اینکه به سورسکد نگاه کنید تابعی بنویسید که یک آرایه چند بعدی رو بگیره و به شکل درخت ترمینالی (مثل کامند tree یا pstree ) ویژوآلایز کنه.

نوشتن کل کلاسها و توابع n_rook و n_queen کلاً یک روز وقت منو گرفت ولی نوشتن این تابع ویژوآل کردن درخت 3 روز ! قطعاً من خیلی فرتوت شدم… ولی بدون الگو گرفتن از سورس کد کسی نوشتنش چالش برانگیز بود! شما هم خودتون رو تست کنید.

[تابعی که نوشتم رو آخر مقاله میفرستم]

و اینکه حالا بریم سراغ توضیحات خیلی مهم:
از اونجایی که PHP زبان مورد علاقه منه، یک کد PHP هم ضمیمه کردم که توش اولاً نود رو پیاده کردم بعدش ساختمان داده درخت رو پیاده کردم و توش از نود استفاده کردم.
آهان یادم رفت بگم ، درخت در علم کامپیوتر یک ساختمان داده یا دیتااستراکچر تلقی میشه مثل هیپ یا هش‌تیبل یا لیست پیوندی یا استک یا … (بعداً توی مقالات دیگه شادی از این‌ها صحبت کردیم)
و بعدش از جناب درخت استفاده کردم و توش تمام جواب‌های ممکن رو بصورت بک‌ترکنیگ تعمیم یافته پیدا کردم و در درخت مذکور ذخیره کردم.
این کد جنبه آموزشی داره ، میخواستم که شما درخت تصمیم جنریت شده رو حتماً ببینید ، وگرنه اگر شخصی بخواد بطور اصولی این مساله رو حل کنه :

اولاً احتمالا نمیاد از بک‌ترکینگ استفاده کنه.
دوماً اگر استفاده کرد، اصلاً اصلاً اصلاً نمیاد از PHP استفاده کنه.
سوماً اگر استفاده کنه ، به هیچ وجه من الوجود درختش رو توی RAM نگه نمیداره! اصلاً نمیتونه نگه داره! بعدش براتون اثبات میکنم که نمیشه! اصلاً درخت رو نمیسازه! ، فقط الگوریتم رو انجام میده و جواب رو مستقیم توی بافر خروجی پرینت میکنه.

وقتی حرف از درخت میشه ، تمام زبانها میکشن عقب ، و راه رو برای یه چیزایی مثل C و ++C باز میکنن ، نه بخاطر اینکه پیرترن و احترامشون واجبه ها ، نه :))
بخاطر اینکه اشاره‌گر دارن...
اشاره گر های زبان ++C [بخونید C] تنها دلیل بقای این زبان هستن. ، قابلیت بسیار خفنیه …. بسیار خفن که در کنار شی گرا بودن زبانی مثل سی‌پلاس بهت اجازه میده که ساختمان داده‌ت رو بصورت بیتوایز ، یعنی در اوج خوارمادر بهینگی پیاده‌سازی کنی.
من قدیما یه کلاس از ساختمان داده درخت توی ++C پیاده کردم در ولی متأسفانه نمیدونم کجاست :))

مساله مهم دیگری که جا داره بگم اینه که من با تغییر چند خط از برنامه مساله nرخ ، n وزیر رو نیز پیاده‌سازی کردم… (دوباره میگم پیاده‌سازی بهینه ای نیستش ، جنبه آموزشی داره)حتما مطالعه‌ش کنین.

نکته مهم دیگه که جای داره من اینجا بگم اینه که من با همین کد بسیار سنگینِ غیر قابل استفاده ، تا 6 رخ رو با سیستم خودم ران گرفتم ، ولی سر 7 رخ سیستمم دود کرد و فریز شد…! (بزارید نگم داستانش غم‌انگیزه !!!‌)
شاید با خودتون بگید : “ هممم :)) مگه 7 رخ چیه که نتونستی :)) “
اجازه بدید که توضیح بدم !

در 7 رخ ، ما یک صفحه شطرنج 7 در 7 داریم پس (با فرض تعمیم ⚠) :

مهره اولو میتونیم توی 49 تا خونه بزاریم
مهره دومو میتونیم توی 36 تا خونه بذاریم
مهره سومو میتونیم توی 25 تا خونه بذاریم
مهره چهارمو میتونیم توی 16 تا خونه بذاریم
مهره پنجمو میتونیم توی 9 تا خونه بذاریم
مهره ششم میتونیم توی 4 تا خونه بذاریم
مهره هفتم میتونیم توی فقط یک خونه بذاریم

نهایتاً درخت ما فقط 1×4×9×16×25×36×49 تا برگ داره ، یعنی 25401600 تا برگ !!!!
خب یعنی توی عمق هفتم فقط 25401600 نود داریم…!
ایضاً تو عمق شیشم هم دقیقاً همونقدر یعنی 25401600 داریم (چرا؟ لختی درنگ...)
توی عمق پنجم 1×4×9×16×25×36 تا نود داریم یعنی 518400 تا
توی عمق چهارم 1×4×9×16×25 تا نود داریم یعنی 14400 تا
توی عمق سوم 1×4×9×16 تا نود داریم یعنی 576 تا
توی عمق دوم 1×4×9 تا نود داریم یعنی 36 تا
توی عمق اول 1×4 تا یعنی 4 تا نود داریم
و نهایتاً توی عمق صفرم که ریشه باشه ، قاعدتاً فقط یک نود داریم.
فلذا میشه گفت که برا 7 رخ ، درخت ما تعدادِ
25401600+ 25401600+ 518400+ 14400+ 576+ 36+ 4 +1
یعنی 51336617 تا … بگو حدود 50 ملیون نود داره :))
طبق محاسباتی که من کردم ، توی این کلاسی که من نوشتم بطور متوسط هر نود خالی حدود 80 بایت فضا از رم رو رزرو میکرد ، فرض کنیم بیشتر هم رزرو نکنه !! :))
51336617×80 میشه 4106929360 بایت یعنی 4010673 مگابایت یعنی 3916 گیگابایت یعنی یچیزی حدود 4 ترابایت :)) شما 4 ترابایت رم داری؟!.. من که ندارم!
برای ران کردن این باید یه سوپرکامپیوتر داشته باشیم!
تازه منتهای مصارف رم جهت فرایند ساخت درخت :))
اگر با ++C هم بطور بهینه بنویسید – مثلاً خیلی شاخ بازی و این داستانا... و هر نودت بشه 15 بایت… (!!!) بازم میشه 734 گیگابایت فضای اشغالی روی رم !!!
پس اونجا دو راه دارید:

یک هارد دیسک بگیرید و درختتونو روش ذخیره کنید ….خخخخخ! (ولی دیگه نمیتونید 8 رخ رو ران کنین !!!! (چرا؟!) )

از خیر ذخیره سازی درخت بگذرید و صرفاً پیمایش و پرینت کنید.

در هر دو صورت رانتایم بالایی خواهد داشت .
مساله nرخ چون جواب زیاد داره اینجوریه ها ، n وزیر جوابهاش خییییلی کمتر هستن و با همین کد پلشت میشه حتی با ذخیره‌سازی درخت رانش کرد، میذارم به عهده شما.

تعجب نکنید که انقدر جوابها فضایی شده….
رشد همه چیز توی این سناریوها نمایی هست ، برای اینکه رشدِ نمایی رو درک کنید یک داستان قدیمی رو بازنشر میکنم - حتماً حتماً حتماً حتماً حتماً بخونید :

*شطرنج یکی از قدیمی ترین بازی های دنیا است و در قرنهای بسیار بسیار دوری اختراع شده است.بنابراین عجیب نیست اگر افسانه های زیادی درباره آن گفته باشند. در اینجا به نقل یکی از آنها می پردازیم.
افسانه می گوید شطرنج ازهندوستان آمده است .شرام شاه (sheoram king) که از حرکات زیرکانه و بیشماری که شخص می توانست با مهره های شطرنج انجام دهد به هیجان آمده بود وقتی که فهمید بنیان گذارش یکی از اتباع همان قلمرو است ،دستور داد مخترع را به حضورش ببرند تا به پاس این اختراع شگفت شخصا به او پاداش دهد.مخترع شطرنج که شخصی بنام سسا (Sessa) بود به حضور شاه بار یافت . شاه با مهربانی گفت :"میل دارم به پاس این اختراع عجیب پاداش خوبی به تو دهم ". دانشمند تعظیم کرد،شاه ادامه داد:"آنقدر غنی هستم که بتوانم بهترین آرزویت را بر آورم،اکنون آنچه می خواهی و لازم داری بگو."
سسا خاموش ماند.
شاه او را تشویق به سخن گفتن کرد و گفت:"شرم نکن ،هر چه می خواهی بگو .برای تامین بهترین آرزوی تو از هیچ چیز دریغ نخواهم کرد."
او جواب داد:"پادشاها لطفت بی پایان است.اما به من فرصتی دهید تا درباره خواسته ام بیندیشم و فردا به عرض برسانم."
روز بعد سسا با درخواست بی نهایت حقیرانه اش شاه را متعجب کرد. او گفت:"ای پادشاه!میل دارم در اولین خانه صفحه شطرنج یک دانه گندم داشته باشم."شاه که تصور می کرد اشتباه شنیده پرسید:"یک دانه گندم معمولی؟" سسا پاسخ داد:" بله شاها در خانه دوم دو دانه ،در خانه سوم چهار دانه ،در خانه چهارم هشت دانه ،در خانه پنجم 16دانه،در خانه ششم 32 دانه و....
شاه با خشم گفت:"کافی است ،دانه های گندمی که برای 64خانه صفحه شطرنج آرزو می کنی خواهی گرفت برای هر خانه دو برابر خانه قبلی. اما بدان که خواهشت شایسته و در خور بخشندگی من نیست. سپس پادشاه گفت :برو !نوکران من کیسه گندمت را برایت می آورند."
سسا تبسمی کرد و رفت جلوی در کاخ به انتظار نشست. هنگام ناهار شاه به یاد سسا افتاد و پرسید که آیا این مخترع پاداش فقیرانه اش را دریافت کرده است، و در جواب به او گفتند: شاها!فرمانت مطاع است .ریاضی دانانت مشغول محاسبه اند تا ببینند چه مقدار گندم باید دریافت کند. شاه روی در هم کشید .زیرا عادت نداشت که اینقدر در اجرای فرمانش تعلل و تاخیر شود.شب قبل از اینکه به بستر برود مجددا پرسید که آیا کیسه گندم سسا داده شده است،ولی گفتند :شاها!ریاضی دانانت دائما در کارند و امیدوارند قبل از طلوع آفتاب کار محاسبه پایان پذیرد.
شاه با خشم گفت:"چرا اینقدر محاسبه می کنند ؟ تا قبل از اینکه از خواب بیدار شوم باید پاداش سسا تا آخرین دانه گندم داده شده باشد،دیگر در این باره دستوری نخواهم داد!" صبح به عرض شاه رساندند که رییس ریاضی دانان دربار اجازه شرفیابی خواسته است.شاه او را به حضور پذیرفت. شاه قبل از اینکه حکیم سخن بگوید گفت:"می خواهم بدانم پاداش محقرانه ای که سسا خواسته بود به او داده شده است؟" حکیم پیر جواب داد:" علت اینکه صبح به این زودی شرفیاب شدم همین است. با کمال وظیفه برای محاسبه گندم سسا کوشیده ایم ،مقدارش بسیار سرسام آور است" .شاه با بی حوصلگی سخن او را قطع کرد و گفت:" هر قدر سرسام آور هم باشد انبارهای قله من می تواند جوابگوی آن باشد.پاداشی که به او قول داده شده است باید به او تحویل شود!
حکیم گفت:"رضایت خاطر و انجام آرزوی سسا در قدرت تو نیست. در تمام انبارهای قله ات مقدار گندمی که سسا خواسته است وجود ندارد. اصولا در تمام خطه ی سلطنت این مقدار گندم یافت نمی شود. در حقیقت دنیا هم چنین گندمی را به خود ندیده است. اگر بخواهی به قولیت وفا کنی باید دستور دهی همه ی زمینهای دنیا به مزارع گندم تبدیل شوند،همه دریاها و اقیانوسها خشک شوند و همه ی یخها و برفهای قطب های دوردست ذوب شوند و بعد اگر تمام این منطق و سرزمینهای عظیم دنیا زیر کشت گندم قرار گیرند شاید ممکن باشد تعداد گندمی که سسا به عنوان پاداش خواسته است به او داده شود."
شاه که حیرت زده به گفتار محاسبش گوش می داد متفکرانه گفت:آن عدد قول پیکر چیست؟

حکیم پاسخ داد:" پادشاها آن عدد 18446744073709551615 است."

این عدد با این صورت بدست امده که باید مجموع اعداد زیر که تشکیل تصاعد هندسی میدهند را به دست آوریم
264 ,....,25 , 24 ,23, 1,2,22
که با استفاده از فرمول مجموع جملات تصاعد هندسی به صورت زیر بدست میاید

(2^64-1)/(2-1) = 18446744073709551615

با محاسبات ، هر یک متر مکعب گندم به طور متوسط شامل15000000 دانه گندم است.بنابراین پاداشی که مخترع شطرنج تقاضا کرده به انباری که 1200000000000 متر مکعب یا 1200کیلومتر مکعب باشد احتیاج است.انباری که برای این کار انتخاب می کنیم اگر 4متر ارتفاع و10متر عرض داشته باشد به طول 30000000کیلومتر یا هشتاد برابر فاصله ی زمین تا ماه خواهد بود.*

این داستان رو چند جا نقل کردن و من نمیتونم بفهمم منبع اصلی کجاست، اگه شما میدونین خبر بدین.

همانا برگهایتان نریخت؟! آیا به عظم رشد نمایی و تخیلی الگوریتمها پی نبردید ؟!

از شوخی گذشته باید راجع به شطرنج و منطق پشتش یه نکته مهمی رو بگم:
شطرنج در زمانی اختراع شد که پادشاهان جنگ‌آوری میکردن و پی کشور گشایی بودن، (انگار که الان مثلاً نیستن ×_× ) فلذا منطق پشتش این هست که اختیارات شاه و ملکه بالاتر از بقیه هست… و ارزش جون شاه و ملکه ملیون ها برابر ارزش جون یه سرباز بیگناه هست… :/ اگه بک ترکینگ یا برنامه‌نویسی با درخت رو یاد بگیریم خوبه اما ، اگر بر این باور باشیم منطق زندگی واقعی هم همینه ، یعنی زندگی جنگه بین عده‌ای از پادشاهانه که باید سربازها فدا بشن تا شاه و ملکه از خطر کیش و مات دور بمونن، اونوقت یادگیری هامون هیچ ارزشی نداره.
ارزش همه آدم‌ها برابر هست ، و زندگی هم بازی شطرنج نیست.

همونطور که گفتم توی سورس‌کدم به مساله n وزیر هم پاسخ دادم و براش یه تابع نوشتم ، منطقش عیناً همون مساله nرخ هست با یخورده تغییر.
چون بچه‌های خوبی هستین ، تغییرشم یه توضیح کوشولو میدم که چیزی بدون توضیح باقی نمونه:
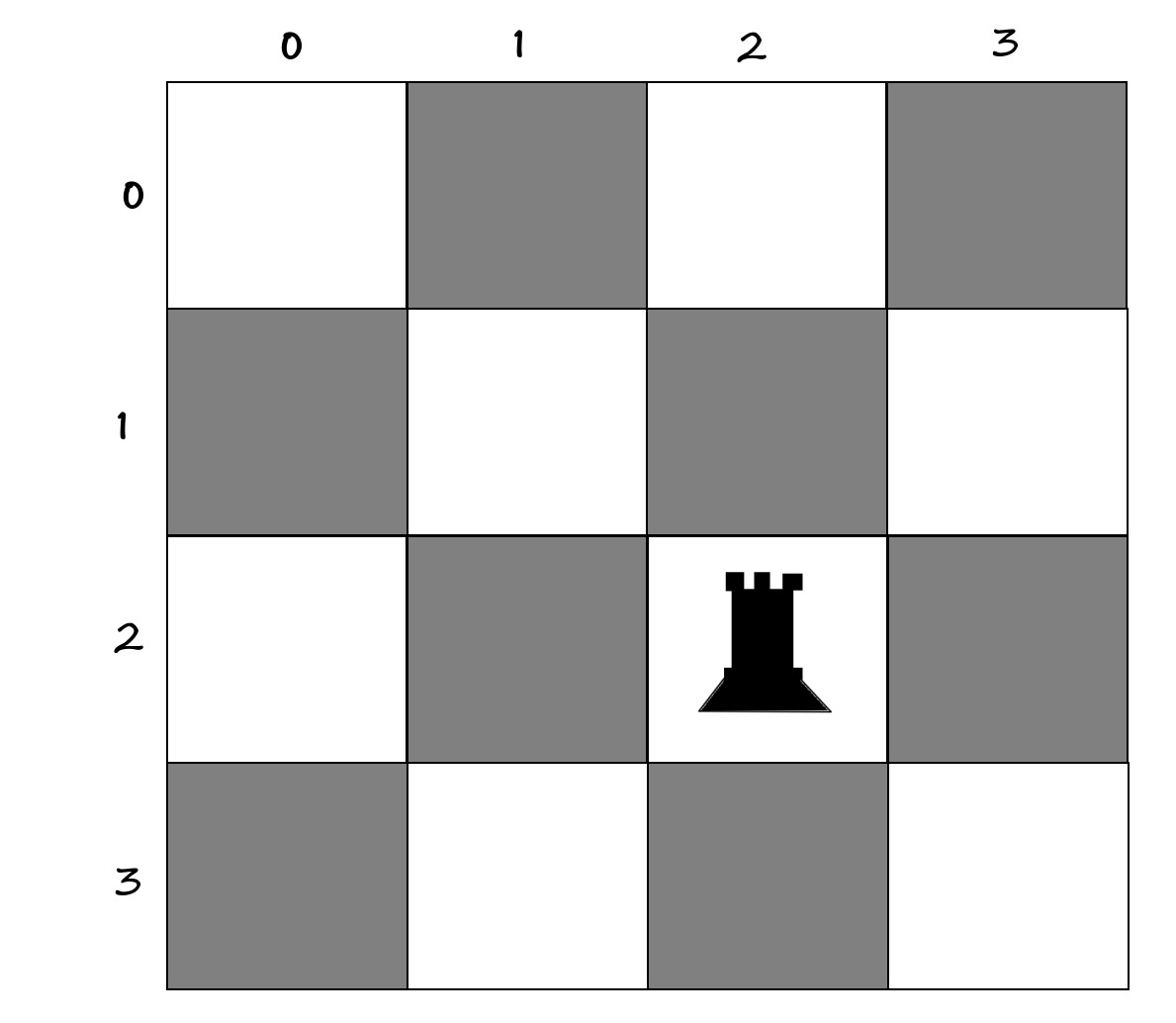
قبلاً که میخواستیم مساله مساله nرخ رو حل کنیم ، فرض کنید مساله 4 رخ :
رخ اول رو مثلا میذاشتیم توی خونه [2,2] :

n rooks one R placement

اونوقت به چه خونه هایی گارد میگرفت؟

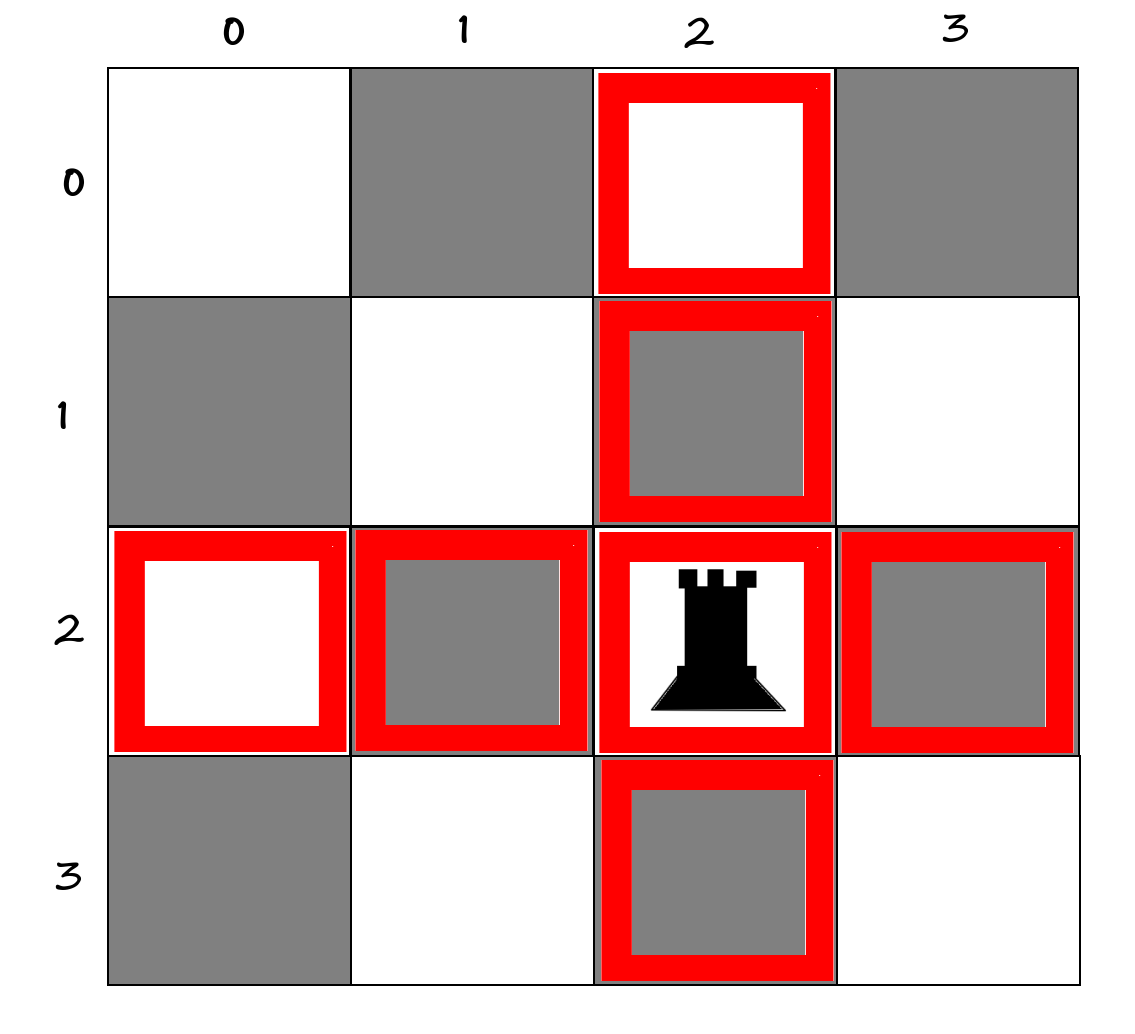
n rooks one R placement

00X0
00X0
XXRX
00X0

توی این خونه هایی که با رنگ قرمز مشخص کردم [X ها] دیگه نمیشد رخ دیگری پلیس کنیم.

تا اینجا که واضحه.

اما فرض کنید توی همین صفحه 4 در 4 ، بخوایم مساله n وزیر رو حل کنیم:

وزیر اول رو مثلا میذاشتیم توی خونه [2,2] :

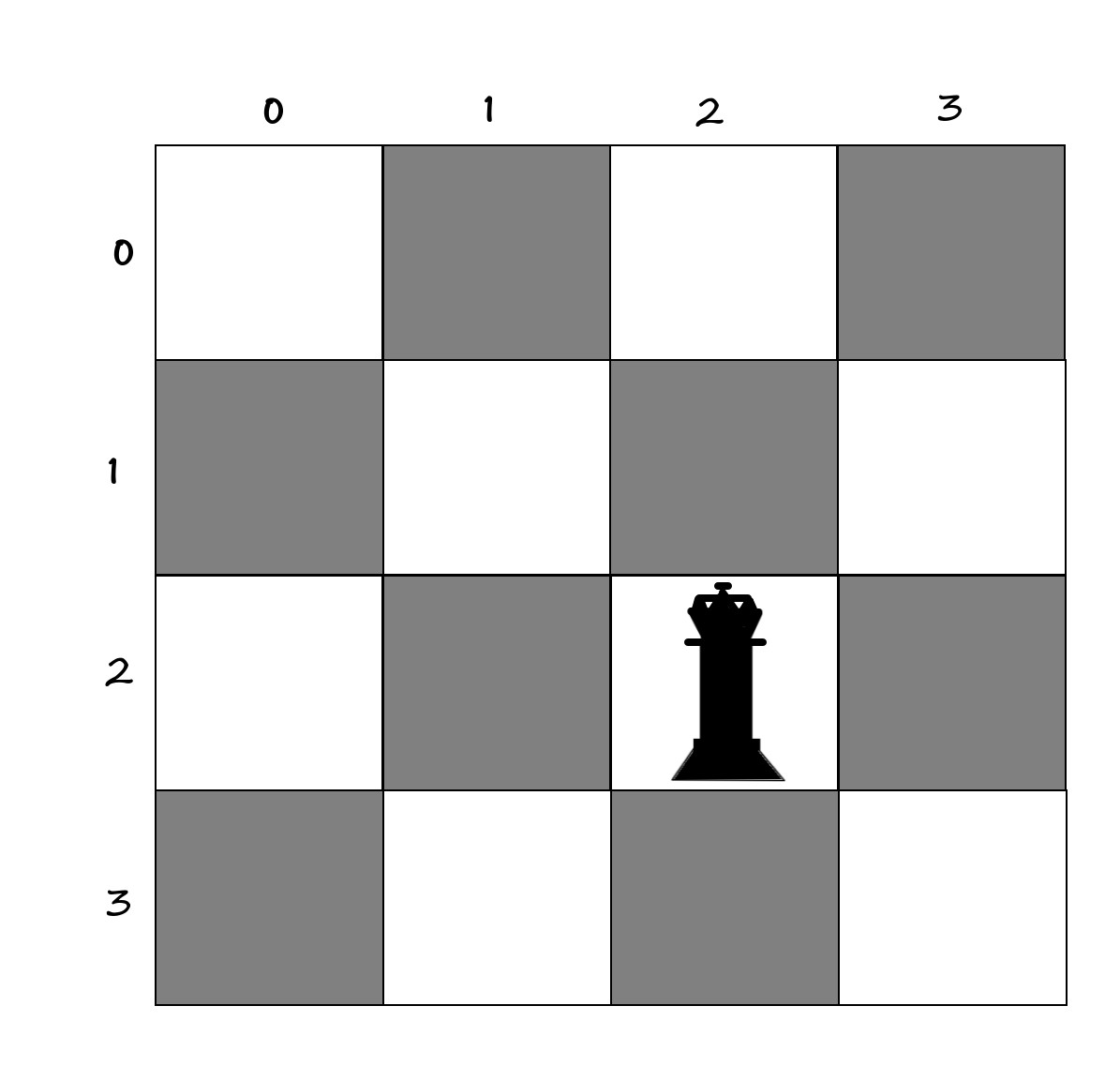
n queens one R placement

حالا این بار به چه خونه هایی گارد میگیره یا بهتره بگم چه خونه هایی غیر قابل سکونت میشن؟

n queens one R placement

X0X0
0XXX
XXQX
0XXX

امیدوارم که متوجه شده باشین چجوری شد، اگه نفهمیدید شکل زیر رو سیاحت بفرمائيد:

n queens one R placement

Z0X0
0ZXZ
XXQX
0ZXZ

1- توی خونه خودش که وزیر دیگری نمیتونه بشینه. (آبی - Q)
2- در راستای عمود و افق خودش گارد داره (قرمز ها - X)
3- در راستای قطر اصلی و فرعی خودش هم گارد داره (صورتی ها - Z)

پس کدمون نسبت به مساله nرخ در اضافه شدن این قسمت صورتی ها تفاوت داره.
برنامه این هم در 2 حالت تمییز قائل شدن/نشدن براتون اجرا میکنم که ببینید.

درباره کدی که نوشتم یه نکته دیگه هم مونده که بهتون بگم اونم این هست که در حالتی که بین مهره‌ها فرقی قائل نمیشیم ، من بعنوان یک فیچر با این هدف که یه نکته یاد بگیرید، یه اطلاعات دیگه هم برای شما چاپ کردم و اون این هست که آیا ماتریس بدست اومده بعنوان جواب نسبت به قطر اصلی قرینه هست یا نه. این قرینه بودن نسبت به قطر اصلی به چه معنیه؟! جلوتر توضیح میدم.

توی بحث ماتریسها ، توی ماتریسهای مربعی هر درایه ای که i اون درایه (شماره سطرش) با j اون درایه (شماره ستونش) برابر باشه ، اصطلاحاً میگیم روی قطر اصلی نشسته.

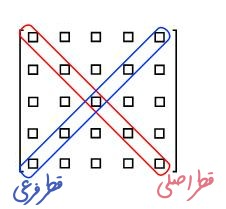
Matrix

X000Z
0X0Z0
00Y00
0Z0X0
Z000X

X = Main diagonal
Z = Antidiagonal

و به تناظرش اون یکی قطر ماتریس رو میگن قطر فرعی.
خیلی راحت…
حالا میخوایم ببینیم این ماتریس بدست اومده نسبت به قطر اصلی قرینه هست یا نه….
منظور چیه ، یعنی هر عنصری اینور قطر اصلی وجود داره ، قرینه‌ش اونور وجود داره یا نه‌،
مثلا:

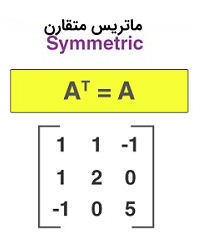
Symmetric Matrix

Symmetric Matrix:

1   1   -1
1   2   0
-1  0   5

A_T = A

نسبت به قطر اصلی قرینه‌ست ، چرا؟ دقت کنید:

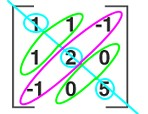
Symmetric Matrix

1   1   -1
1   2   0
-1  0   5

ولی ماتریس زیر قرینه نیست:

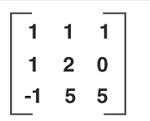
Symmetric Matrix

1   1   1
1   2   0
-1  0   5

خب واضحه که به ماتریسی که نسبت به قطر اصلی قرینه باشه میگن متقارن یا سمتریک.

اگه بخوام یخورده تخصصی به بحث ماتریس های متقارن توی سؤال خودمون نگاه کنم، اون پاسخ‌هایی متقارن هستن که چه از سمت بازیکن سفید به صفحه نگاه کنیم و چه از سمت بازیکن سیاه به صفحه نگاه کنیم ، یه حالت رو ببینیم. اینکه منظورم چیه رو با شکل نشون میدم.
برنامه هر ماتریسی که متقارن باشه رو (توی حالت تمییز قائل نشدن فقط. وگرنه توی حالت تمییز قائل شدن که تقارن معنی نمیده {چرا؟ - اگه به این بتونید پاسخ بدید یعنی بحث رو درک کردید.}) بالای اون ماتریس یه عبارت symmetric چاپ میکنه.
مثلاً توی 4 رخ ، اگر برنامه رو اجرا کنید ، میبینید از 24 تا جواب تولید شده ، 10 تاش متقارن هستن ، مثلاً یکی از اون متقارن ها این هست:

_______
**symmetric**
0 0 0 1 
0 1 0 0 
0 0 1 0 
1 0 0 0 
_______

الان دقت کنید، ببینید نسبت به قطر اصلی متقارنه.

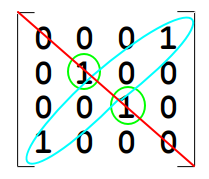
Symmetric Matrix

حالا دقیقاً همین حالت رو روی صفحه شطرنج ببینید:

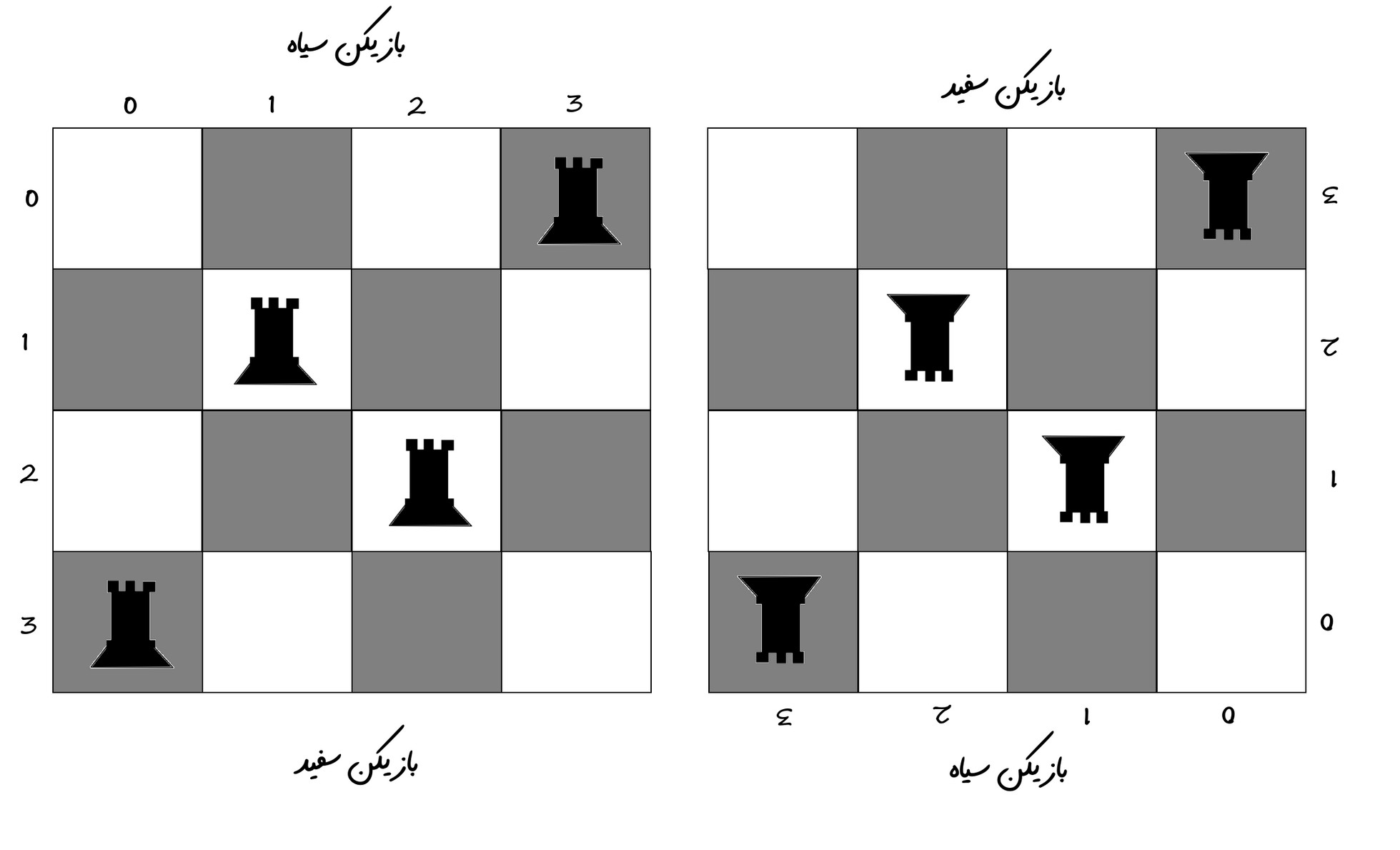
Symmetric Chessboard

White
0 0 0 1 
0 1 0 0 
0 0 1 0 
1 0 0 0
Black


Black
0 0 0 1 
0 1 0 0 
0 0 1 0 
1 0 0 0
White

دقیقاً همون عکس رو 180 درجه روتیت کردم که منظورم رو متوجه بشید.
پس این حالات متقارن هم برنامه واستون مشخص میکنه.

خب خب خب…
خسته شدیم 😅
این توضیحات فقط مژه بر همزدنی از الگوریتم عقبگرد یا back-tracking بود.

حالا یه توضیح درباره نحوه ران کردن کد بدم ، و خروجی 3 قسمت اول رو به عنوان حسن ختام این سؤال طولانی و سکسی که با خودش هزاران نکته رو می آموزه خدمتتون نشون بدم :

برای ران کردن فقط کافیه که back_tracking.php رو ران کنید. توش دوبار هر دو تابع رو فراخونی کردم ، هم تابع n وزیر و هم تابع مساله nرخ که بار اول با اعمال «بی تفاوتی» (شرط سوالمون) مساله رو حل میکنه و بار دوم با اعمال تمییز و تفاوت.

[سورسکد و آخر مقاله الصاق کردم]

من اجرای کد رو :

برای 1 رخ شرح میدم – بی تفاوت
برای 1 رخ شرح میدم – با تفاوت
برای 1 وزیر شرح میدم – بی تفاوت
برای 1 وزیر شرح میدم – با تفاوت
برای 2 رخ شرح میدم – بی تفاوت
برای 2 رخ شرح میدم – با تفاوت
برای 2 وزیر شرح میدم – بی تفاوت
برای 2 وزیر شرح میدم – با تفاوت
برای 3 رخ شرح میدم – بی تفاوت
برای 3 رخ شرح میدم – با تفاوت
برای 3 وزیر شرح میدم – بی تفاوت
برای 3 وزیر شرح میدم – با تفاوت
چون دوستون دارم ، برای 4 رخ هم شرح میدم – بی‌تفاوت
چون خیلی دوستون دارم ، برای 4 رخ هم شرح میدم – با تفاوت
چون خیلی خیلی دوستون دارم ، برای 4 وزیر هم شرح میدم – بی تفاوت
و چون خیلی خیلی خیلی دوستون دارم ، برای 4 وزیر هم شرح میدم – با تفاوت

مساله nرخ - برای n = 1 (بی‌تفاوت):
تابع رو بصورت زیر فراخونی کنید:

n_rooks( 1 );

و خروجی این قسمت :

behrad@TadavomnisT:~/Desktop$ php back_tracking.php 

** 1 ROOKS ** (no distinguish between rooks)
Building empty matrix...
Building decision tree...
Printing decision tree :
.
└── "root"
    └── [0,0]

Printing all possible solutions :
**symmetric**
1 
_
Number of answers : 1
Number of symmetric answers : 1
___________________________________
behrad@TadavomnisT:~/Desktop$

مساله nرخ - برای n = 1 (باتفاوت):
تابع رو بصورت زیر فراخونی کنید:

n_rooks( 1 , true ); //distinguish between rooks

و خروجی این قسمت :

behrad@TadavomnisT:~/Desktop$ php back_tracking.php 

** 1 ROOKS ** (distinguishing between rooks)
Building empty matrix...
Building decision tree...
Printing decision tree :
.
└── "root"
    └── [0,0]

Printing all possible solutions :
1 
_
Number of answers : 1
___________________________________
behrad@TadavomnisT:~/Desktop$

مساله nوزیر - برای n = 1 (بی‌تفاوت):
تابع رو بصورت زیر فراخونی کنید:

n_queens( 1 );

و خروجی این قسمت :

behrad@TadavomnisT:~/Desktop$ php back_tracking.php 

** 1 QUEENS ** (no distinguish between queens)
Building empty matrix...
Building decision tree...
Printing decision tree :
.
└── "root"
    └── [0,0]

Printing all possible solutions :
**symmetric**
1 
_
Number of answers : 1
Number of symmetric answers : 1
___________________________________
behrad@TadavomnisT:~/Desktop$

مساله nوزیر - برای n = 1 (باتفاوت):
تابع رو بصورت زیر فراخونی کنید:

n_queens( 1 , true ); //distinguish between queens

و خروجی این قسمت :

behrad@TadavomnisT:~/Desktop$ php back_tracking.php 

** 1 QUEENS ** (distinguishing between queens)
Building empty matrix...
Building decision tree...
Printing decision tree :
.
└── "root"
    └── [0,0]

Printing all possible solutions :
1 
_
Number of answers : 1
___________________________________
behrad@TadavomnisT:~/Desktop$

مساله nرخ - برای n = 2 (بی‌تفاوت):
تابع رو بصورت زیر فراخونی کنید:

n_rooks( 2 );

و خروجی این قسمت :

behrad@TadavomnisT:~/Desktop$ php back_tracking.php 

** 2 ROOKS ** (no distinguish between rooks)
Building empty matrix...
Building decision tree...
Printing decision tree :
.
└── "root"
    ├── [0,0]
    │   └── [1,1]
    ├── [0,1]
    │   └── [1,0]
    ├── [1,0]
    │   └── [0,1]
    └── [1,1]
        └── [0,0]

Printing all possible solutions :
**symmetric**
1 0 
0 1 
___
**symmetric**
0 1 
1 0 
___
Number of answers : 2
Number of symmetric answers : 2
___________________________________
behrad@TadavomnisT:~/Desktop$

مساله nرخ - برای n = 2 (باتفاوت):
تابع رو بصورت زیر فراخونی کنید:

n_rooks( 2 , true ); //distinguish between rooks

و خروجی این قسمت :

behrad@TadavomnisT:~/Desktop$ php back_tracking.php 

** 2 ROOKS ** (distinguishing between rooks)
Building empty matrix...
Building decision tree...
Printing decision tree :
.
└── "root"
    ├── [0,0]
    │   └── [1,1]
    ├── [0,1]
    │   └── [1,0]
    ├── [1,0]
    │   └── [0,1]
    └── [1,1]
        └── [0,0]

Printing all possible solutions :
1 0 
0 2 
___
0 1 
2 0 
___
0 2 
1 0 
___
2 0 
0 1 
___
Number of answers : 4
___________________________________
behrad@TadavomnisT:~/Desktop$

مساله nوزیر - برای n = 2 (بی‌تفاوت):
تابع رو بصورت زیر فراخونی کنید:

n_queens( 2 );

و خروجی این قسمت :

behrad@TadavomnisT:~/Desktop$ php back_tracking.php 

** 2 QUEENS ** (no distinguish between queens)
Building empty matrix...
Building decision tree...
Printing decision tree :
.
└── "root"
    ├── [0,0]
    ├── [0,1]
    ├── [1,0]
    └── [1,1]

Printing all possible solutions :
Number of answers : 0
Number of symmetric answers : 0
___________________________________
behrad@TadavomnisT:~/Desktop$

مساله nوزیر - برای n = 2 (باتفاوت):
تابع رو بصورت زیر فراخونی کنید:

n_queens( 2 , true ); //distinguish between queens

و خروجی این قسمت :

behrad@TadavomnisT:~/Desktop$ php back_tracking.php 

** 2 QUEENS ** (distinguishing between queens)
Building empty matrix...
Building decision tree...
Printing decision tree :
.
└── "root"
    ├── [0,0]
    ├── [0,1]
    ├── [1,0]
    └── [1,1]

Printing all possible solutions :
Number of answers : 0
___________________________________
behrad@TadavomnisT:~/Desktop$

مساله nرخ - برای n = 3 (بی‌تفاوت):
تابع رو بصورت زیر فراخونی کنید:

n_rooks( 3 );

و خروجی این قسمت :

behrad@TadavomnisT:~/Desktop$ php back_tracking.php 

** 3 ROOKS ** (no distinguish between rooks)
Building empty matrix...
Building decision tree...
Printing decision tree :
.
└── "root"
    ├── [0,0]
    │   ├── [1,1]
    │   │   └── [2,2]
    │   ├── [1,2]
    │   │   └── [2,1]
    │   ├── [2,1]
    │   │   └── [1,2]
    │   └── [2,2]
    │       └── [1,1]
    ├── [0,1]
    │   ├── [1,0]
    │   │   └── [2,2]
    │   ├── [1,2]
    │   │   └── [2,0]
    │   ├── [2,0]
    │   │   └── [1,2]
    │   └── [2,2]
    │       └── [1,0]
    ├── [0,2]
    │   ├── [1,0]
    │   │   └── [2,1]
    │   ├── [1,1]
    │   │   └── [2,0]
    │   ├── [2,0]
    │   │   └── [1,1]
    │   └── [2,1]
    │       └── [1,0]
    ├── [1,0]
    │   ├── [0,1]
    │   │   └── [2,2]
    │   ├── [0,2]
    │   │   └── [2,1]
    │   ├── [2,1]
    │   │   └── [0,2]
    │   └── [2,2]
    │       └── [0,1]
    ├── [1,1]
    │   ├── [0,0]
    │   │   └── [2,2]
    │   ├── [0,2]
    │   │   └── [2,0]
    │   ├── [2,0]
    │   │   └── [0,2]
    │   └── [2,2]
    │       └── [0,0]
    ├── [1,2]
    │   ├── [0,0]
    │   │   └── [2,1]
    │   ├── [0,1]
    │   │   └── [2,0]
    │   ├── [2,0]
    │   │   └── [0,1]
    │   └── [2,1]
    │       └── [0,0]
    ├── [2,0]
    │   ├── [0,1]
    │   │   └── [1,2]
    │   ├── [0,2]
    │   │   └── [1,1]
    │   ├── [1,1]
    │   │   └── [0,2]
    │   └── [1,2]
    │       └── [0,1]
    ├── [2,1]
    │   ├── [0,0]
    │   │   └── [1,2]
    │   ├── [0,2]
    │   │   └── [1,0]
    │   ├── [1,0]
    │   │   └── [0,2]
    │   └── [1,2]
    │       └── [0,0]
    └── [2,2]
        ├── [0,0]
        │   └── [1,1]
        ├── [0,1]
        │   └── [1,0]
        ├── [1,0]
        │   └── [0,1]
        └── [1,1]
            └── [0,0]

Printing all possible solutions :
**symmetric**
1 0 0 
0 1 0 
0 0 1 
_____
**symmetric**
1 0 0 
0 0 1 
0 1 0 
_____
**symmetric**
0 1 0 
1 0 0 
0 0 1 
_____
0 1 0 
0 0 1 
1 0 0 
_____
0 0 1 
1 0 0 
0 1 0 
_____
**symmetric**
0 0 1 
0 1 0 
1 0 0 
_____
Number of answers : 6
Number of symmetric answers : 4
___________________________________
behrad@TadavomnisT:~/Desktop$

مساله nرخ - برای n = 3 (باتفاوت):
تابع رو بصورت زیر فراخونی کنید:

n_rooks( 3 , true ); //distinguish between rooks

و خروجی این قسمت :

behrad@TadavomnisT:~/Desktop$ php back_tracking.php 

** 3 ROOKS ** (distinguishing between rooks)
Building empty matrix...
Building decision tree...
Printing decision tree :
.
└── "root"
    ├── [0,0]
    │   ├── [1,1]
    │   │   └── [2,2]
    │   ├── [1,2]
    │   │   └── [2,1]
    │   ├── [2,1]
    │   │   └── [1,2]
    │   └── [2,2]
    │       └── [1,1]
    ├── [0,1]
    │   ├── [1,0]
    │   │   └── [2,2]
    │   ├── [1,2]
    │   │   └── [2,0]
    │   ├── [2,0]
    │   │   └── [1,2]
    │   └── [2,2]
    │       └── [1,0]
    ├── [0,2]
    │   ├── [1,0]
    │   │   └── [2,1]
    │   ├── [1,1]
    │   │   └── [2,0]
    │   ├── [2,0]
    │   │   └── [1,1]
    │   └── [2,1]
    │       └── [1,0]
    ├── [1,0]
    │   ├── [0,1]
    │   │   └── [2,2]
    │   ├── [0,2]
    │   │   └── [2,1]
    │   ├── [2,1]
    │   │   └── [0,2]
    │   └── [2,2]
    │       └── [0,1]
    ├── [1,1]
    │   ├── [0,0]
    │   │   └── [2,2]
    │   ├── [0,2]
    │   │   └── [2,0]
    │   ├── [2,0]
    │   │   └── [0,2]
    │   └── [2,2]
    │       └── [0,0]
    ├── [1,2]
    │   ├── [0,0]
    │   │   └── [2,1]
    │   ├── [0,1]
    │   │   └── [2,0]
    │   ├── [2,0]
    │   │   └── [0,1]
    │   └── [2,1]
    │       └── [0,0]
    ├── [2,0]
    │   ├── [0,1]
    │   │   └── [1,2]
    │   ├── [0,2]
    │   │   └── [1,1]
    │   ├── [1,1]
    │   │   └── [0,2]
    │   └── [1,2]
    │       └── [0,1]
    ├── [2,1]
    │   ├── [0,0]
    │   │   └── [1,2]
    │   ├── [0,2]
    │   │   └── [1,0]
    │   ├── [1,0]
    │   │   └── [0,2]
    │   └── [1,2]
    │       └── [0,0]
    └── [2,2]
        ├── [0,0]
        │   └── [1,1]
        ├── [0,1]
        │   └── [1,0]
        ├── [1,0]
        │   └── [0,1]
        └── [1,1]
            └── [0,0]

Printing all possible solutions :
1 0 0 
0 2 0 
0 0 3 
_____
1 0 0 
0 0 2 
0 3 0 
_____
1 0 0 
0 0 3 
0 2 0 
_____
1 0 0 
0 3 0 
0 0 2 
_____
0 1 0 
2 0 0 
0 0 3 
_____
0 1 0 
0 0 2 
3 0 0 
_____
0 1 0 
0 0 3 
2 0 0 
_____
0 1 0 
3 0 0 
0 0 2 
_____
0 0 1 
2 0 0 
0 3 0 
_____
0 0 1 
0 2 0 
3 0 0 
_____
0 0 1 
0 3 0 
2 0 0 
_____
0 0 1 
3 0 0 
0 2 0 
_____
0 2 0 
1 0 0 
0 0 3 
_____
0 0 2 
1 0 0 
0 3 0 
_____
0 0 3 
1 0 0 
0 2 0 
_____
0 3 0 
1 0 0 
0 0 2 
_____
2 0 0 
0 1 0 
0 0 3 
_____
0 0 2 
0 1 0 
3 0 0 
_____
0 0 3 
0 1 0 
2 0 0 
_____
3 0 0 
0 1 0 
0 0 2 
_____
2 0 0 
0 0 1 
0 3 0 
_____
0 2 0 
0 0 1 
3 0 0 
_____
0 3 0 
0 0 1 
2 0 0 
_____
3 0 0 
0 0 1 
0 2 0 
_____
0 2 0 
0 0 3 
1 0 0 
_____
0 0 2 
0 3 0 
1 0 0 
_____
0 0 3 
0 2 0 
1 0 0 
_____
0 3 0 
0 0 2 
1 0 0 
_____
2 0 0 
0 0 3 
0 1 0 
_____
0 0 2 
3 0 0 
0 1 0 
_____
0 0 3 
2 0 0 
0 1 0 
_____
3 0 0 
0 0 2 
0 1 0 
_____
2 0 0 
0 3 0 
0 0 1 
_____
0 2 0 
3 0 0 
0 0 1 
_____
0 3 0 
2 0 0 
0 0 1 
_____
3 0 0 
0 2 0 
0 0 1 
_____
Number of answers : 36
___________________________________
behrad@TadavomnisT:~/Desktop$

مساله nوزیر - برای n = 3 (بی‌تفاوت):
تابع رو بصورت زیر فراخونی کنید:

n_queens( 3 );

و خروجی این قسمت :

behrad@TadavomnisT:~/Desktop$ php back_tracking.php 

** 3 QUEENS ** (no distinguish between queens)
Building empty matrix...
Building decision tree...
Printing decision tree :
.
└── "root"
    ├── [0,0]
    │   ├── [1,2]
    │   └── [2,1]
    ├── [0,1]
    │   ├── [2,0]
    │   └── [2,2]
    ├── [0,2]
    │   ├── [1,0]
    │   └── [2,1]
    ├── [1,0]
    │   ├── [0,2]
    │   └── [2,2]
    ├── [1,1]
    ├── [1,2]
    │   ├── [0,0]
    │   └── [2,0]
    ├── [2,0]
    │   ├── [0,1]
    │   └── [1,2]
    ├── [2,1]
    │   ├── [0,0]
    │   └── [0,2]
    └── [2,2]
        ├── [0,1]
        └── [1,0]

Printing all possible solutions :
Number of answers : 0
Number of symmetric answers : 0
___________________________________
behrad@TadavomnisT:~/Desktop$

مساله nوزیر - برای n = 3 (باتفاوت):
تابع رو بصورت زیر فراخونی کنید:

n_queens( 3 , true ); //distinguish between queens

و خروجی این قسمت :

behrad@TadavomnisT:~/Desktop$ php back_tracking.php 

** 3 QUEENS ** (distinguishing between queens)
Building empty matrix...
Building decision tree...
Printing decision tree :
.
└── "root"
    ├── [0,0]
    │   ├── [1,2]
    │   └── [2,1]
    ├── [0,1]
    │   ├── [2,0]
    │   └── [2,2]
    ├── [0,2]
    │   ├── [1,0]
    │   └── [2,1]
    ├── [1,0]
    │   ├── [0,2]
    │   └── [2,2]
    ├── [1,1]
    ├── [1,2]
    │   ├── [0,0]
    │   └── [2,0]
    ├── [2,0]
    │   ├── [0,1]
    │   └── [1,2]
    ├── [2,1]
    │   ├── [0,0]
    │   └── [0,2]
    └── [2,2]
        ├── [0,1]
        └── [1,0]

Printing all possible solutions :
Number of answers : 0
___________________________________
behrad@TadavomnisT:~/Desktop$

مساله nرخ - برای n = 4 (بی‌تفاوت):
تابع رو بصورت زیر فراخونی کنید:

n_rooks( 4 );

و خروجی این قسمت :

behrad@TadavomnisT:~/Desktop$ php back_tracking.php 

** 4 ROOKS ** (no distinguish between rooks)
Building empty matrix...
Building decision tree...
Printing decision tree :
.
└── "root"
    ├── [0,0]
    │   ├── [1,1]
    │   │   ├── [2,2]
    │   │   │   └── [3,3]
    │   │   ├── [2,3]
    │   │   │   └── [3,2]
    │   │   ├── [3,2]
    │   │   │   └── [2,3]
    │   │   └── [3,3]
    │   │       └── [2,2]
    │   ├── [1,2]
    │   │   ├── [2,1]
    │   │   │   └── [3,3]
    │   │   ├── [2,3]
    │   │   │   └── [3,1]
    │   │   ├── [3,1]
    │   │   │   └── [2,3]
    │   │   └── [3,3]
    │   │       └── [2,1]
    │   ├── [1,3]
    │   │   ├── [2,1]
    │   │   │   └── [3,2]
    │   │   ├── [2,2]
    │   │   │   └── [3,1]
    │   │   ├── [3,1]
    │   │   │   └── [2,2]
    │   │   └── [3,2]
    │   │       └── [2,1]
    │   ├── [2,1]
    │   │   ├── [1,2]
    │   │   │   └── [3,3]
    │   │   ├── [1,3]
    │   │   │   └── [3,2]
    │   │   ├── [3,2]
    │   │   │   └── [1,3]
    │   │   └── [3,3]
    │   │       └── [1,2]
    │   ├── [2,2]
    │   │   ├── [1,1]
    │   │   │   └── [3,3]
    │   │   ├── [1,3]
    │   │   │   └── [3,1]
    │   │   ├── [3,1]
    │   │   │   └── [1,3]
    │   │   └── [3,3]
    │   │       └── [1,1]
    │   ├── [2,3]
    │   │   ├── [1,1]
    │   │   │   └── [3,2]
    │   │   ├── [1,2]
    │   │   │   └── [3,1]
    │   │   ├── [3,1]
    │   │   │   └── [1,2]
    │   │   └── [3,2]
    │   │       └── [1,1]
    │   ├── [3,1]
    │   │   ├── [1,2]
    │   │   │   └── [2,3]
    │   │   ├── [1,3]
    │   │   │   └── [2,2]
    │   │   ├── [2,2]
    │   │   │   └── [1,3]
    │   │   └── [2,3]
    │   │       └── [1,2]
    │   ├── [3,2]
    │   │   ├── [1,1]
    │   │   │   └── [2,3]
    │   │   ├── [1,3]
    │   │   │   └── [2,1]
    │   │   ├── [2,1]
    │   │   │   └── [1,3]
    │   │   └── [2,3]
    │   │       └── [1,1]
    │   └── [3,3]
    │       ├── [1,1]
    │       │   └── [2,2]
    │       ├── [1,2]
    │       │   └── [2,1]
    │       ├── [2,1]
    │       │   └── [1,2]
    │       └── [2,2]
    │           └── [1,1]
    ├── [0,1]
    │   ├── [1,0]
    │   │   ├── [2,2]
    │   │   │   └── [3,3]
    │   │   ├── [2,3]
    │   │   │   └── [3,2]
    │   │   ├── [3,2]
    │   │   │   └── [2,3]
    │   │   └── [3,3]
    │   │       └── [2,2]
    │   ├── [1,2]
    │   │   ├── [2,0]
    │   │   │   └── [3,3]
    │   │   ├── [2,3]
    │   │   │   └── [3,0]
    │   │   ├── [3,0]
    │   │   │   └── [2,3]
    │   │   └── [3,3]
    │   │       └── [2,0]
    │   ├── [1,3]
    │   │   ├── [2,0]
    │   │   │   └── [3,2]
    │   │   ├── [2,2]
    │   │   │   └── [3,0]
    │   │   ├── [3,0]
    │   │   │   └── [2,2]
    │   │   └── [3,2]
    │   │       └── [2,0]
    │   ├── [2,0]
    │   │   ├── [1,2]
    │   │   │   └── [3,3]
    │   │   ├── [1,3]
    │   │   │   └── [3,2]
    │   │   ├── [3,2]
    │   │   │   └── [1,3]
    │   │   └── [3,3]
    │   │       └── [1,2]
    │   ├── [2,2]
    │   │   ├── [1,0]
    │   │   │   └── [3,3]
    │   │   ├── [1,3]
    │   │   │   └── [3,0]
    │   │   ├── [3,0]
    │   │   │   └── [1,3]
    │   │   └── [3,3]
    │   │       └── [1,0]
    │   ├── [2,3]
    │   │   ├── [1,0]
    │   │   │   └── [3,2]
    │   │   ├── [1,2]
    │   │   │   └── [3,0]
    │   │   ├── [3,0]
    │   │   │   └── [1,2]
    │   │   └── [3,2]
    │   │       └── [1,0]
    │   ├── [3,0]
    │   │   ├── [1,2]
    │   │   │   └── [2,3]
    │   │   ├── [1,3]
    │   │   │   └── [2,2]
    │   │   ├── [2,2]
    │   │   │   └── [1,3]
    │   │   └── [2,3]
    │   │       └── [1,2]
    │   ├── [3,2]
    │   │   ├── [1,0]
    │   │   │   └── [2,3]
    │   │   ├── [1,3]
    │   │   │   └── [2,0]
    │   │   ├── [2,0]
    │   │   │   └── [1,3]
    │   │   └── [2,3]
    │   │       └── [1,0]
    │   └── [3,3]
    │       ├── [1,0]
    │       │   └── [2,2]
    │       ├── [1,2]
    │       │   └── [2,0]
    │       ├── [2,0]
    │       │   └── [1,2]
    │       └── [2,2]
    │           └── [1,0]
    ├── [0,2]
    │   ├── [1,0]
    │   │   ├── [2,1]
    │   │   │   └── [3,3]
    │   │   ├── [2,3]
    │   │   │   └── [3,1]
    │   │   ├── [3,1]
    │   │   │   └── [2,3]
    │   │   └── [3,3]
    │   │       └── [2,1]
    │   ├── [1,1]
    │   │   ├── [2,0]
    │   │   │   └── [3,3]
    │   │   ├── [2,3]
    │   │   │   └── [3,0]
    │   │   ├── [3,0]
    │   │   │   └── [2,3]
    │   │   └── [3,3]
    │   │       └── [2,0]
    │   ├── [1,3]
    │   │   ├── [2,0]
    │   │   │   └── [3,1]
    │   │   ├── [2,1]
    │   │   │   └── [3,0]
    │   │   ├── [3,0]
    │   │   │   └── [2,1]
    │   │   └── [3,1]
    │   │       └── [2,0]
    │   ├── [2,0]
    │   │   ├── [1,1]
    │   │   │   └── [3,3]
    │   │   ├── [1,3]
    │   │   │   └── [3,1]
    │   │   ├── [3,1]
    │   │   │   └── [1,3]
    │   │   └── [3,3]
    │   │       └── [1,1]
    │   ├── [2,1]
    │   │   ├── [1,0]
    │   │   │   └── [3,3]
    │   │   ├── [1,3]
    │   │   │   └── [3,0]
    │   │   ├── [3,0]
    │   │   │   └── [1,3]
    │   │   └── [3,3]
    │   │       └── [1,0]
    │   ├── [2,3]
    │   │   ├── [1,0]
    │   │   │   └── [3,1]
    │   │   ├── [1,1]
    │   │   │   └── [3,0]
    │   │   ├── [3,0]
    │   │   │   └── [1,1]
    │   │   └── [3,1]
    │   │       └── [1,0]
    │   ├── [3,0]
    │   │   ├── [1,1]
    │   │   │   └── [2,3]
    │   │   ├── [1,3]
    │   │   │   └── [2,1]
    │   │   ├── [2,1]
    │   │   │   └── [1,3]
    │   │   └── [2,3]
    │   │       └── [1,1]
    │   ├── [3,1]
    │   │   ├── [1,0]
    │   │   │   └── [2,3]
    │   │   ├── [1,3]
    │   │   │   └── [2,0]
    │   │   ├── [2,0]
    │   │   │   └── [1,3]
    │   │   └── [2,3]
    │   │       └── [1,0]
    │   └── [3,3]
    │       ├── [1,0]
    │       │   └── [2,1]
    │       ├── [1,1]
    │       │   └── [2,0]
    │       ├── [2,0]
    │       │   └── [1,1]
    │       └── [2,1]
    │           └── [1,0]
    ├── [0,3]
    │   ├── [1,0]
    │   │   ├── [2,1]
    │   │   │   └── [3,2]
    │   │   ├── [2,2]
    │   │   │   └── [3,1]
    │   │   ├── [3,1]
    │   │   │   └── [2,2]
    │   │   └── [3,2]
    │   │       └── [2,1]
    │   ├── [1,1]
    │   │   ├── [2,0]
    │   │   │   └── [3,2]
    │   │   ├── [2,2]
    │   │   │   └── [3,0]
    │   │   ├── [3,0]
    │   │   │   └── [2,2]
    │   │   └── [3,2]
    │   │       └── [2,0]
    │   ├── [1,2]
    │   │   ├── [2,0]
    │   │   │   └── [3,1]
    │   │   ├── [2,1]
    │   │   │   └── [3,0]
    │   │   ├── [3,0]
    │   │   │   └── [2,1]
    │   │   └── [3,1]
    │   │       └── [2,0]
    │   ├── [2,0]
    │   │   ├── [1,1]
    │   │   │   └── [3,2]
    │   │   ├── [1,2]
    │   │   │   └── [3,1]
    │   │   ├── [3,1]
    │   │   │   └── [1,2]
    │   │   └── [3,2]
    │   │       └── [1,1]
    │   ├── [2,1]
    │   │   ├── [1,0]
    │   │   │   └── [3,2]
    │   │   ├── [1,2]
    │   │   │   └── [3,0]
    │   │   ├── [3,0]
    │   │   │   └── [1,2]
    │   │   └── [3,2]
    │   │       └── [1,0]
    │   ├── [2,2]
    │   │   ├── [1,0]
    │   │   │   └── [3,1]
    │   │   ├── [1,1]
    │   │   │   └── [3,0]
    │   │   ├── [3,0]
    │   │   │   └── [1,1]
    │   │   └── [3,1]
    │   │       └── [1,0]
    │   ├── [3,0]
    │   │   ├── [1,1]
    │   │   │   └── [2,2]
    │   │   ├── [1,2]
    │   │   │   └── [2,1]
    │   │   ├── [2,1]
    │   │   │   └── [1,2]
    │   │   └── [2,2]
    │   │       └── [1,1]
    │   ├── [3,1]
    │   │   ├── [1,0]
    │   │   │   └── [2,2]
    │   │   ├── [1,2]
    │   │   │   └── [2,0]
    │   │   ├── [2,0]
    │   │   │   └── [1,2]
    │   │   └── [2,2]
    │   │       └── [1,0]
    │   └── [3,2]
    │       ├── [1,0]
    │       │   └── [2,1]
    │       ├── [1,1]
    │       │   └── [2,0]
    │       ├── [2,0]
    │       │   └── [1,1]
    │       └── [2,1]
    │           └── [1,0]
    ├── [1,0]
    │   ├── [0,1]
    │   │   ├── [2,2]
    │   │   │   └── [3,3]
    │   │   ├── [2,3]
    │   │   │   └── [3,2]
    │   │   ├── [3,2]
    │   │   │   └── [2,3]
    │   │   └── [3,3]
    │   │       └── [2,2]
    │   ├── [0,2]
    │   │   ├── [2,1]
    │   │   │   └── [3,3]
    │   │   ├── [2,3]
    │   │   │   └── [3,1]
    │   │   ├── [3,1]
    │   │   │   └── [2,3]
    │   │   └── [3,3]
    │   │       └── [2,1]
    │   ├── [0,3]
    │   │   ├── [2,1]
    │   │   │   └── [3,2]
    │   │   ├── [2,2]
    │   │   │   └── [3,1]
    │   │   ├── [3,1]
    │   │   │   └── [2,2]
    │   │   └── [3,2]
    │   │       └── [2,1]
    │   ├── [2,1]
    │   │   ├── [0,2]
    │   │   │   └── [3,3]
    │   │   ├── [0,3]
    │   │   │   └── [3,2]
    │   │   ├── [3,2]
    │   │   │   └── [0,3]
    │   │   └── [3,3]
    │   │       └── [0,2]
    │   ├── [2,2]
    │   │   ├── [0,1]
    │   │   │   └── [3,3]
    │   │   ├── [0,3]
    │   │   │   └── [3,1]
    │   │   ├── [3,1]
    │   │   │   └── [0,3]
    │   │   └── [3,3]
    │   │       └── [0,1]
    │   ├── [2,3]
    │   │   ├── [0,1]
    │   │   │   └── [3,2]
    │   │   ├── [0,2]
    │   │   │   └── [3,1]
    │   │   ├── [3,1]
    │   │   │   └── [0,2]
    │   │   └── [3,2]
    │   │       └── [0,1]
    │   ├── [3,1]
    │   │   ├── [0,2]
    │   │   │   └── [2,3]
    │   │   ├── [0,3]
    │   │   │   └── [2,2]
    │   │   ├── [2,2]
    │   │   │   └── [0,3]
    │   │   └── [2,3]
    │   │       └── [0,2]
    │   ├── [3,2]
    │   │   ├── [0,1]
    │   │   │   └── [2,3]
    │   │   ├── [0,3]
    │   │   │   └── [2,1]
    │   │   ├── [2,1]
    │   │   │   └── [0,3]
    │   │   └── [2,3]
    │   │       └── [0,1]
    │   └── [3,3]
    │       ├── [0,1]
    │       │   └── [2,2]
    │       ├── [0,2]
    │       │   └── [2,1]
    │       ├── [2,1]
    │       │   └── [0,2]
    │       └── [2,2]
    │           └── [0,1]
    ├── [1,1]
    │   ├── [0,0]
    │   │   ├── [2,2]
    │   │   │   └── [3,3]
    │   │   ├── [2,3]
    │   │   │   └── [3,2]
    │   │   ├── [3,2]
    │   │   │   └── [2,3]
    │   │   └── [3,3]
    │   │       └── [2,2]
    │   ├── [0,2]
    │   │   ├── [2,0]
    │   │   │   └── [3,3]
    │   │   ├── [2,3]
    │   │   │   └── [3,0]
    │   │   ├── [3,0]
    │   │   │   └── [2,3]
    │   │   └── [3,3]
    │   │       └── [2,0]
    │   ├── [0,3]
    │   │   ├── [2,0]
    │   │   │   └── [3,2]
    │   │   ├── [2,2]
    │   │   │   └── [3,0]
    │   │   ├── [3,0]
    │   │   │   └── [2,2]
    │   │   └── [3,2]
    │   │       └── [2,0]
    │   ├── [2,0]
    │   │   ├── [0,2]
    │   │   │   └── [3,3]
    │   │   ├── [0,3]
    │   │   │   └── [3,2]
    │   │   ├── [3,2]
    │   │   │   └── [0,3]
    │   │   └── [3,3]
    │   │       └── [0,2]
    │   ├── [2,2]
    │   │   ├── [0,0]
    │   │   │   └── [3,3]
    │   │   ├── [0,3]
    │   │   │   └── [3,0]
    │   │   ├── [3,0]
    │   │   │   └── [0,3]
    │   │   └── [3,3]
    │   │       └── [0,0]
    │   ├── [2,3]
    │   │   ├── [0,0]
    │   │   │   └── [3,2]
    │   │   ├── [0,2]
    │   │   │   └── [3,0]
    │   │   ├── [3,0]
    │   │   │   └── [0,2]
    │   │   └── [3,2]
    │   │       └── [0,0]
    │   ├── [3,0]
    │   │   ├── [0,2]
    │   │   │   └── [2,3]
    │   │   ├── [0,3]
    │   │   │   └── [2,2]
    │   │   ├── [2,2]
    │   │   │   └── [0,3]
    │   │   └── [2,3]
    │   │       └── [0,2]
    │   ├── [3,2]
    │   │   ├── [0,0]
    │   │   │   └── [2,3]
    │   │   ├── [0,3]
    │   │   │   └── [2,0]
    │   │   ├── [2,0]
    │   │   │   └── [0,3]
    │   │   └── [2,3]
    │   │       └── [0,0]
    │   └── [3,3]
    │       ├── [0,0]
    │       │   └── [2,2]
    │       ├── [0,2]
    │       │   └── [2,0]
    │       ├── [2,0]
    │       │   └── [0,2]
    │       └── [2,2]
    │           └── [0,0]
    ├── [1,2]
    │   ├── [0,0]
    │   │   ├── [2,1]
    │   │   │   └── [3,3]
    │   │   ├── [2,3]
    │   │   │   └── [3,1]
    │   │   ├── [3,1]
    │   │   │   └── [2,3]
    │   │   └── [3,3]
    │   │       └── [2,1]
    │   ├── [0,1]
    │   │   ├── [2,0]
    │   │   │   └── [3,3]
    │   │   ├── [2,3]
    │   │   │   └── [3,0]
    │   │   ├── [3,0]
    │   │   │   └── [2,3]
    │   │   └── [3,3]
    │   │       └── [2,0]
    │   ├── [0,3]
    │   │   ├── [2,0]
    │   │   │   └── [3,1]
    │   │   ├── [2,1]
    │   │   │   └── [3,0]
    │   │   ├── [3,0]
    │   │   │   └── [2,1]
    │   │   └── [3,1]
    │   │       └── [2,0]
    │   ├── [2,0]
    │   │   ├── [0,1]
    │   │   │   └── [3,3]
    │   │   ├── [0,3]
    │   │   │   └── [3,1]
    │   │   ├── [3,1]
    │   │   │   └── [0,3]
    │   │   └── [3,3]
    │   │       └── [0,1]
    │   ├── [2,1]
    │   │   ├── [0,0]
    │   │   │   └── [3,3]
    │   │   ├── [0,3]
    │   │   │   └── [3,0]
    │   │   ├── [3,0]
    │   │   │   └── [0,3]
    │   │   └── [3,3]
    │   │       └── [0,0]
    │   ├── [2,3]
    │   │   ├── [0,0]
    │   │   │   └── [3,1]
    │   │   ├── [0,1]
    │   │   │   └── [3,0]
    │   │   ├── [3,0]
    │   │   │   └── [0,1]
    │   │   └── [3,1]
    │   │       └── [0,0]
    │   ├── [3,0]
    │   │   ├── [0,1]
    │   │   │   └── [2,3]
    │   │   ├── [0,3]
    │   │   │   └── [2,1]
    │   │   ├── [2,1]
    │   │   │   └── [0,3]
    │   │   └── [2,3]
    │   │       └── [0,1]
    │   ├── [3,1]
    │   │   ├── [0,0]
    │   │   │   └── [2,3]
    │   │   ├── [0,3]
    │   │   │   └── [2,0]
    │   │   ├── [2,0]
    │   │   │   └── [0,3]
    │   │   └── [2,3]
    │   │       └── [0,0]
    │   └── [3,3]
    │       ├── [0,0]
    │       │   └── [2,1]
    │       ├── [0,1]
    │       │   └── [2,0]
    │       ├── [2,0]
    │       │   └── [0,1]
    │       └── [2,1]
    │           └── [0,0]
    ├── [1,3]
    │   ├── [0,0]
    │   │   ├── [2,1]
    │   │   │   └── [3,2]
    │   │   ├── [2,2]
    │   │   │   └── [3,1]
    │   │   ├── [3,1]
    │   │   │   └── [2,2]
    │   │   └── [3,2]
    │   │       └── [2,1]
    │   ├── [0,1]
    │   │   ├── [2,0]
    │   │   │   └── [3,2]
    │   │   ├── [2,2]
    │   │   │   └── [3,0]
    │   │   ├── [3,0]
    │   │   │   └── [2,2]
    │   │   └── [3,2]
    │   │       └── [2,0]
    │   ├── [0,2]
    │   │   ├── [2,0]
    │   │   │   └── [3,1]
    │   │   ├── [2,1]
    │   │   │   └── [3,0]
    │   │   ├── [3,0]
    │   │   │   └── [2,1]
    │   │   └── [3,1]
    │   │       └── [2,0]
    │   ├── [2,0]
    │   │   ├── [0,1]
    │   │   │   └── [3,2]
    │   │   ├── [0,2]
    │   │   │   └── [3,1]
    │   │   ├── [3,1]
    │   │   │   └── [0,2]
    │   │   └── [3,2]
    │   │       └── [0,1]
    │   ├── [2,1]
    │   │   ├── [0,0]
    │   │   │   └── [3,2]
    │   │   ├── [0,2]
    │   │   │   └── [3,0]
    │   │   ├── [3,0]
    │   │   │   └── [0,2]
    │   │   └── [3,2]
    │   │       └── [0,0]
    │   ├── [2,2]
    │   │   ├── [0,0]
    │   │   │   └── [3,1]
    │   │   ├── [0,1]
    │   │   │   └── [3,0]
    │   │   ├── [3,0]
    │   │   │   └── [0,1]
    │   │   └── [3,1]
    │   │       └── [0,0]
    │   ├── [3,0]
    │   │   ├── [0,1]
    │   │   │   └── [2,2]
    │   │   ├── [0,2]
    │   │   │   └── [2,1]
    │   │   ├── [2,1]
    │   │   │   └── [0,2]
    │   │   └── [2,2]
    │   │       └── [0,1]
    │   ├── [3,1]
    │   │   ├── [0,0]
    │   │   │   └── [2,2]
    │   │   ├── [0,2]
    │   │   │   └── [2,0]
    │   │   ├── [2,0]
    │   │   │   └── [0,2]
    │   │   └── [2,2]
    │   │       └── [0,0]
    │   └── [3,2]
    │       ├── [0,0]
    │       │   └── [2,1]
    │       ├── [0,1]
    │       │   └── [2,0]
    │       ├── [2,0]
    │       │   └── [0,1]
    │       └── [2,1]
    │           └── [0,0]
    ├── [2,0]
    │   ├── [0,1]
    │   │   ├── [1,2]
    │   │   │   └── [3,3]
    │   │   ├── [1,3]
    │   │   │   └── [3,2]
    │   │   ├── [3,2]
    │   │   │   └── [1,3]
    │   │   └── [3,3]
    │   │       └── [1,2]
    │   ├── [0,2]
    │   │   ├── [1,1]
    │   │   │   └── [3,3]
    │   │   ├── [1,3]
    │   │   │   └── [3,1]
    │   │   ├── [3,1]
    │   │   │   └── [1,3]
    │   │   └── [3,3]
    │   │       └── [1,1]
    │   ├── [0,3]
    │   │   ├── [1,1]
    │   │   │   └── [3,2]
    │   │   ├── [1,2]
    │   │   │   └── [3,1]
    │   │   ├── [3,1]
    │   │   │   └── [1,2]
    │   │   └── [3,2]
    │   │       └── [1,1]
    │   ├── [1,1]
    │   │   ├── [0,2]
    │   │   │   └── [3,3]
    │   │   ├── [0,3]
    │   │   │   └── [3,2]
    │   │   ├── [3,2]
    │   │   │   └── [0,3]
    │   │   └── [3,3]
    │   │       └── [0,2]
    │   ├── [1,2]
    │   │   ├── [0,1]
    │   │   │   └── [3,3]
    │   │   ├── [0,3]
    │   │   │   └── [3,1]
    │   │   ├── [3,1]
    │   │   │   └── [0,3]
    │   │   └── [3,3]
    │   │       └── [0,1]
    │   ├── [1,3]
    │   │   ├── [0,1]
    │   │   │   └── [3,2]
    │   │   ├── [0,2]
    │   │   │   └── [3,1]
    │   │   ├── [3,1]
    │   │   │   └── [0,2]
    │   │   └── [3,2]
    │   │       └── [0,1]
    │   ├── [3,1]
    │   │   ├── [0,2]
    │   │   │   └── [1,3]
    │   │   ├── [0,3]
    │   │   │   └── [1,2]
    │   │   ├── [1,2]
    │   │   │   └── [0,3]
    │   │   └── [1,3]
    │   │       └── [0,2]
    │   ├── [3,2]
    │   │   ├── [0,1]
    │   │   │   └── [1,3]
    │   │   ├── [0,3]
    │   │   │   └── [1,1]
    │   │   ├── [1,1]
    │   │   │   └── [0,3]
    │   │   └── [1,3]
    │   │       └── [0,1]
    │   └── [3,3]
    │       ├── [0,1]
    │       │   └── [1,2]
    │       ├── [0,2]
    │       │   └── [1,1]
    │       ├── [1,1]
    │       │   └── [0,2]
    │       └── [1,2]
    │           └── [0,1]
    ├── [2,1]
    │   ├── [0,0]
    │   │   ├── [1,2]
    │   │   │   └── [3,3]
    │   │   ├── [1,3]
    │   │   │   └── [3,2]
    │   │   ├── [3,2]
    │   │   │   └── [1,3]
    │   │   └── [3,3]
    │   │       └── [1,2]
    │   ├── [0,2]
    │   │   ├── [1,0]
    │   │   │   └── [3,3]
    │   │   ├── [1,3]
    │   │   │   └── [3,0]
    │   │   ├── [3,0]
    │   │   │   └── [1,3]
    │   │   └── [3,3]
    │   │       └── [1,0]
    │   ├── [0,3]
    │   │   ├── [1,0]
    │   │   │   └── [3,2]
    │   │   ├── [1,2]
    │   │   │   └── [3,0]
    │   │   ├── [3,0]
    │   │   │   └── [1,2]
    │   │   └── [3,2]
    │   │       └── [1,0]
    │   ├── [1,0]
    │   │   ├── [0,2]
    │   │   │   └── [3,3]
    │   │   ├── [0,3]
    │   │   │   └── [3,2]
    │   │   ├── [3,2]
    │   │   │   └── [0,3]
    │   │   └── [3,3]
    │   │       └── [0,2]
    │   ├── [1,2]
    │   │   ├── [0,0]
    │   │   │   └── [3,3]
    │   │   ├── [0,3]
    │   │   │   └── [3,0]
    │   │   ├── [3,0]
    │   │   │   └── [0,3]
    │   │   └── [3,3]
    │   │       └── [0,0]
    │   ├── [1,3]
    │   │   ├── [0,0]
    │   │   │   └── [3,2]
    │   │   ├── [0,2]
    │   │   │   └── [3,0]
    │   │   ├── [3,0]
    │   │   │   └── [0,2]
    │   │   └── [3,2]
    │   │       └── [0,0]
    │   ├── [3,0]
    │   │   ├── [0,2]
    │   │   │   └── [1,3]
    │   │   ├── [0,3]
    │   │   │   └── [1,2]
    │   │   ├── [1,2]
    │   │   │   └── [0,3]
    │   │   └── [1,3]
    │   │       └── [0,2]
    │   ├── [3,2]
    │   │   ├── [0,0]
    │   │   │   └── [1,3]
    │   │   ├── [0,3]
    │   │   │   └── [1,0]
    │   │   ├── [1,0]
    │   │   │   └── [0,3]
    │   │   └── [1,3]
    │   │       └── [0,0]
    │   └── [3,3]
    │       ├── [0,0]
    │       │   └── [1,2]
    │       ├── [0,2]
    │       │   └── [1,0]
    │       ├── [1,0]
    │       │   └── [0,2]
    │       └── [1,2]
    │           └── [0,0]
    ├── [2,2]
    │   ├── [0,0]
    │   │   ├── [1,1]
    │   │   │   └── [3,3]
    │   │   ├── [1,3]
    │   │   │   └── [3,1]
    │   │   ├── [3,1]
    │   │   │   └── [1,3]
    │   │   └── [3,3]
    │   │       └── [1,1]
    │   ├── [0,1]
    │   │   ├── [1,0]
    │   │   │   └── [3,3]
    │   │   ├── [1,3]
    │   │   │   └── [3,0]
    │   │   ├── [3,0]
    │   │   │   └── [1,3]
    │   │   └── [3,3]
    │   │       └── [1,0]
    │   ├── [0,3]
    │   │   ├── [1,0]
    │   │   │   └── [3,1]
    │   │   ├── [1,1]
    │   │   │   └── [3,0]
    │   │   ├── [3,0]
    │   │   │   └── [1,1]
    │   │   └── [3,1]
    │   │       └── [1,0]
    │   ├── [1,0]
    │   │   ├── [0,1]
    │   │   │   └── [3,3]
    │   │   ├── [0,3]
    │   │   │   └── [3,1]
    │   │   ├── [3,1]
    │   │   │   └── [0,3]
    │   │   └── [3,3]
    │   │       └── [0,1]
    │   ├── [1,1]
    │   │   ├── [0,0]
    │   │   │   └── [3,3]
    │   │   ├── [0,3]
    │   │   │   └── [3,0]
    │   │   ├── [3,0]
    │   │   │   └── [0,3]
    │   │   └── [3,3]
    │   │       └── [0,0]
    │   ├── [1,3]
    │   │   ├── [0,0]
    │   │   │   └── [3,1]
    │   │   ├── [0,1]
    │   │   │   └── [3,0]
    │   │   ├── [3,0]
    │   │   │   └── [0,1]
    │   │   └── [3,1]
    │   │       └── [0,0]
    │   ├── [3,0]
    │   │   ├── [0,1]
    │   │   │   └── [1,3]
    │   │   ├── [0,3]
    │   │   │   └── [1,1]
    │   │   ├── [1,1]
    │   │   │   └── [0,3]
    │   │   └── [1,3]
    │   │       └── [0,1]
    │   ├── [3,1]
    │   │   ├── [0,0]
    │   │   │   └── [1,3]
    │   │   ├── [0,3]
    │   │   │   └── [1,0]
    │   │   ├── [1,0]
    │   │   │   └── [0,3]
    │   │   └── [1,3]
    │   │       └── [0,0]
    │   └── [3,3]
    │       ├── [0,0]
    │       │   └── [1,1]
    │       ├── [0,1]
    │       │   └── [1,0]
    │       ├── [1,0]
    │       │   └── [0,1]
    │       └── [1,1]
    │           └── [0,0]
    ├── [2,3]
    │   ├── [0,0]
    │   │   ├── [1,1]
    │   │   │   └── [3,2]
    │   │   ├── [1,2]
    │   │   │   └── [3,1]
    │   │   ├── [3,1]
    │   │   │   └── [1,2]
    │   │   └── [3,2]
    │   │       └── [1,1]
    │   ├── [0,1]
    │   │   ├── [1,0]
    │   │   │   └── [3,2]
    │   │   ├── [1,2]
    │   │   │   └── [3,0]
    │   │   ├── [3,0]
    │   │   │   └── [1,2]
    │   │   └── [3,2]
    │   │       └── [1,0]
    │   ├── [0,2]
    │   │   ├── [1,0]
    │   │   │   └── [3,1]
    │   │   ├── [1,1]
    │   │   │   └── [3,0]
    │   │   ├── [3,0]
    │   │   │   └── [1,1]
    │   │   └── [3,1]
    │   │       └── [1,0]
    │   ├── [1,0]
    │   │   ├── [0,1]
    │   │   │   └── [3,2]
    │   │   ├── [0,2]
    │   │   │   └── [3,1]
    │   │   ├── [3,1]
    │   │   │   └── [0,2]
    │   │   └── [3,2]
    │   │       └── [0,1]
    │   ├── [1,1]
    │   │   ├── [0,0]
    │   │   │   └── [3,2]
    │   │   ├── [0,2]
    │   │   │   └── [3,0]
    │   │   ├── [3,0]
    │   │   │   └── [0,2]
    │   │   └── [3,2]
    │   │       └── [0,0]
    │   ├── [1,2]
    │   │   ├── [0,0]
    │   │   │   └── [3,1]
    │   │   ├── [0,1]
    │   │   │   └── [3,0]
    │   │   ├── [3,0]
    │   │   │   └── [0,1]
    │   │   └── [3,1]
    │   │       └── [0,0]
    │   ├── [3,0]
    │   │   ├── [0,1]
    │   │   │   └── [1,2]
    │   │   ├── [0,2]
    │   │   │   └── [1,1]
    │   │   ├── [1,1]
    │   │   │   └── [0,2]
    │   │   └── [1,2]
    │   │       └── [0,1]
    │   ├── [3,1]
    │   │   ├── [0,0]
    │   │   │   └── [1,2]
    │   │   ├── [0,2]
    │   │   │   └── [1,0]
    │   │   ├── [1,0]
    │   │   │   └── [0,2]
    │   │   └── [1,2]
    │   │       └── [0,0]
    │   └── [3,2]
    │       ├── [0,0]
    │       │   └── [1,1]
    │       ├── [0,1]
    │       │   └── [1,0]
    │       ├── [1,0]
    │       │   └── [0,1]
    │       └── [1,1]
    │           └── [0,0]
    ├── [3,0]
    │   ├── [0,1]
    │   │   ├── [1,2]
    │   │   │   └── [2,3]
    │   │   ├── [1,3]
    │   │   │   └── [2,2]
    │   │   ├── [2,2]
    │   │   │   └── [1,3]
    │   │   └── [2,3]
    │   │       └── [1,2]
    │   ├── [0,2]
    │   │   ├── [1,1]
    │   │   │   └── [2,3]
    │   │   ├── [1,3]
    │   │   │   └── [2,1]
    │   │   ├── [2,1]
    │   │   │   └── [1,3]
    │   │   └── [2,3]
    │   │       └── [1,1]
    │   ├── [0,3]
    │   │   ├── [1,1]
    │   │   │   └── [2,2]
    │   │   ├── [1,2]
    │   │   │   └── [2,1]
    │   │   ├── [2,1]
    │   │   │   └── [1,2]
    │   │   └── [2,2]
    │   │       └── [1,1]
    │   ├── [1,1]
    │   │   ├── [0,2]
    │   │   │   └── [2,3]
    │   │   ├── [0,3]
    │   │   │   └── [2,2]
    │   │   ├── [2,2]
    │   │   │   └── [0,3]
    │   │   └── [2,3]
    │   │       └── [0,2]
    │   ├── [1,2]
    │   │   ├── [0,1]
    │   │   │   └── [2,3]
    │   │   ├── [0,3]
    │   │   │   └── [2,1]
    │   │   ├── [2,1]
    │   │   │   └── [0,3]
    │   │   └── [2,3]
    │   │       └── [0,1]
    │   ├── [1,3]
    │   │   ├── [0,1]
    │   │   │   └── [2,2]
    │   │   ├── [0,2]
    │   │   │   └── [2,1]
    │   │   ├── [2,1]
    │   │   │   └── [0,2]
    │   │   └── [2,2]
    │   │       └── [0,1]
    │   ├── [2,1]
    │   │   ├── [0,2]
    │   │   │   └── [1,3]
    │   │   ├── [0,3]
    │   │   │   └── [1,2]
    │   │   ├── [1,2]
    │   │   │   └── [0,3]
    │   │   └── [1,3]
    │   │       └── [0,2]
    │   ├── [2,2]
    │   │   ├── [0,1]
    │   │   │   └── [1,3]
    │   │   ├── [0,3]
    │   │   │   └── [1,1]
    │   │   ├── [1,1]
    │   │   │   └── [0,3]
    │   │   └── [1,3]
    │   │       └── [0,1]
    │   └── [2,3]
    │       ├── [0,1]
    │       │   └── [1,2]
    │       ├── [0,2]
    │       │   └── [1,1]
    │       ├── [1,1]
    │       │   └── [0,2]
    │       └── [1,2]
    │           └── [0,1]
    ├── [3,1]
    │   ├── [0,0]
    │   │   ├── [1,2]
    │   │   │   └── [2,3]
    │   │   ├── [1,3]
    │   │   │   └── [2,2]
    │   │   ├── [2,2]
    │   │   │   └── [1,3]
    │   │   └── [2,3]
    │   │       └── [1,2]
    │   ├── [0,2]
    │   │   ├── [1,0]
    │   │   │   └── [2,3]
    │   │   ├── [1,3]
    │   │   │   └── [2,0]
    │   │   ├── [2,0]
    │   │   │   └── [1,3]
    │   │   └── [2,3]
    │   │       └── [1,0]
    │   ├── [0,3]
    │   │   ├── [1,0]
    │   │   │   └── [2,2]
    │   │   ├── [1,2]
    │   │   │   └── [2,0]
    │   │   ├── [2,0]
    │   │   │   └── [1,2]
    │   │   └── [2,2]
    │   │       └── [1,0]
    │   ├── [1,0]
    │   │   ├── [0,2]
    │   │   │   └── [2,3]
    │   │   ├── [0,3]
    │   │   │   └── [2,2]
    │   │   ├── [2,2]
    │   │   │   └── [0,3]
    │   │   └── [2,3]
    │   │       └── [0,2]
    │   ├── [1,2]
    │   │   ├── [0,0]
    │   │   │   └── [2,3]
    │   │   ├── [0,3]
    │   │   │   └── [2,0]
    │   │   ├── [2,0]
    │   │   │   └── [0,3]
    │   │   └── [2,3]
    │   │       └── [0,0]
    │   ├── [1,3]
    │   │   ├── [0,0]
    │   │   │   └── [2,2]
    │   │   ├── [0,2]
    │   │   │   └── [2,0]
    │   │   ├── [2,0]
    │   │   │   └── [0,2]
    │   │   └── [2,2]
    │   │       └── [0,0]
    │   ├── [2,0]
    │   │   ├── [0,2]
    │   │   │   └── [1,3]
    │   │   ├── [0,3]
    │   │   │   └── [1,2]
    │   │   ├── [1,2]
    │   │   │   └── [0,3]
    │   │   └── [1,3]
    │   │       └── [0,2]
    │   ├── [2,2]
    │   │   ├── [0,0]
    │   │   │   └── [1,3]
    │   │   ├── [0,3]
    │   │   │   └── [1,0]
    │   │   ├── [1,0]
    │   │   │   └── [0,3]
    │   │   └── [1,3]
    │   │       └── [0,0]
    │   └── [2,3]
    │       ├── [0,0]
    │       │   └── [1,2]
    │       ├── [0,2]
    │       │   └── [1,0]
    │       ├── [1,0]
    │       │   └── [0,2]
    │       └── [1,2]
    │           └── [0,0]
    ├── [3,2]
    │   ├── [0,0]
    │   │   ├── [1,1]
    │   │   │   └── [2,3]
    │   │   ├── [1,3]
    │   │   │   └── [2,1]
    │   │   ├── [2,1]
    │   │   │   └── [1,3]
    │   │   └── [2,3]
    │   │       └── [1,1]
    │   ├── [0,1]
    │   │   ├── [1,0]
    │   │   │   └── [2,3]
    │   │   ├── [1,3]
    │   │   │   └── [2,0]
    │   │   ├── [2,0]
    │   │   │   └── [1,3]
    │   │   └── [2,3]
    │   │       └── [1,0]
    │   ├── [0,3]
    │   │   ├── [1,0]
    │   │   │   └── [2,1]
    │   │   ├── [1,1]
    │   │   │   └── [2,0]
    │   │   ├── [2,0]
    │   │   │   └── [1,1]
    │   │   └── [2,1]
    │   │       └── [1,0]
    │   ├── [1,0]
    │   │   ├── [0,1]
    │   │   │   └── [2,3]
    │   │   ├── [0,3]
    │   │   │   └── [2,1]
    │   │   ├── [2,1]
    │   │   │   └── [0,3]
    │   │   └── [2,3]
    │   │       └── [0,1]
    │   ├── [1,1]
    │   │   ├── [0,0]
    │   │   │   └── [2,3]
    │   │   ├── [0,3]
    │   │   │   └── [2,0]
    │   │   ├── [2,0]
    │   │   │   └── [0,3]
    │   │   └── [2,3]
    │   │       └── [0,0]
    │   ├── [1,3]
    │   │   ├── [0,0]
    │   │   │   └── [2,1]
    │   │   ├── [0,1]
    │   │   │   └── [2,0]
    │   │   ├── [2,0]
    │   │   │   └── [0,1]
    │   │   └── [2,1]
    │   │       └── [0,0]
    │   ├── [2,0]
    │   │   ├── [0,1]
    │   │   │   └── [1,3]
    │   │   ├── [0,3]
    │   │   │   └── [1,1]
    │   │   ├── [1,1]
    │   │   │   └── [0,3]
    │   │   └── [1,3]
    │   │       └── [0,1]
    │   ├── [2,1]
    │   │   ├── [0,0]
    │   │   │   └── [1,3]
    │   │   ├── [0,3]
    │   │   │   └── [1,0]
    │   │   ├── [1,0]
    │   │   │   └── [0,3]
    │   │   └── [1,3]
    │   │       └── [0,0]
    │   └── [2,3]
    │       ├── [0,0]
    │       │   └── [1,1]
    │       ├── [0,1]
    │       │   └── [1,0]
    │       ├── [1,0]
    │       │   └── [0,1]
    │       └── [1,1]
    │           └── [0,0]
    └── [3,3]
        ├── [0,0]
        │   ├── [1,1]
        │   │   └── [2,2]
        │   ├── [1,2]
        │   │   └── [2,1]
        │   ├── [2,1]
        │   │   └── [1,2]
        │   └── [2,2]
        │       └── [1,1]
        ├── [0,1]
        │   ├── [1,0]
        │   │   └── [2,2]
        │   ├── [1,2]
        │   │   └── [2,0]
        │   ├── [2,0]
        │   │   └── [1,2]
        │   └── [2,2]
        │       └── [1,0]
        ├── [0,2]
        │   ├── [1,0]
        │   │   └── [2,1]
        │   ├── [1,1]
        │   │   └── [2,0]
        │   ├── [2,0]
        │   │   └── [1,1]
        │   └── [2,1]
        │       └── [1,0]
        ├── [1,0]
        │   ├── [0,1]
        │   │   └── [2,2]
        │   ├── [0,2]
        │   │   └── [2,1]
        │   ├── [2,1]
        │   │   └── [0,2]
        │   └── [2,2]
        │       └── [0,1]
        ├── [1,1]
        │   ├── [0,0]
        │   │   └── [2,2]
        │   ├── [0,2]
        │   │   └── [2,0]
        │   ├── [2,0]
        │   │   └── [0,2]
        │   └── [2,2]
        │       └── [0,0]
        ├── [1,2]
        │   ├── [0,0]
        │   │   └── [2,1]
        │   ├── [0,1]
        │   │   └── [2,0]
        │   ├── [2,0]
        │   │   └── [0,1]
        │   └── [2,1]
        │       └── [0,0]
        ├── [2,0]
        │   ├── [0,1]
        │   │   └── [1,2]
        │   ├── [0,2]
        │   │   └── [1,1]
        │   ├── [1,1]
        │   │   └── [0,2]
        │   └── [1,2]
        │       └── [0,1]
        ├── [2,1]
        │   ├── [0,0]
        │   │   └── [1,2]
        │   ├── [0,2]
        │   │   └── [1,0]
        │   ├── [1,0]
        │   │   └── [0,2]
        │   └── [1,2]
        │       └── [0,0]
        └── [2,2]
            ├── [0,0]
            │   └── [1,1]
            ├── [0,1]
            │   └── [1,0]
            ├── [1,0]
            │   └── [0,1]
            └── [1,1]
                └── [0,0]

Printing all possible solutions :
**symmetric**
1 0 0 0 
0 1 0 0 
0 0 1 0 
0 0 0 1 
_______
**symmetric**
1 0 0 0 
0 1 0 0 
0 0 0 1 
0 0 1 0 
_______
**symmetric**
1 0 0 0 
0 0 1 0 
0 1 0 0 
0 0 0 1 
_______
1 0 0 0 
0 0 1 0 
0 0 0 1 
0 1 0 0 
_______
1 0 0 0 
0 0 0 1 
0 1 0 0 
0 0 1 0 
_______
**symmetric**
1 0 0 0 
0 0 0 1 
0 0 1 0 
0 1 0 0 
_______
**symmetric**
0 1 0 0 
1 0 0 0 
0 0 1 0 
0 0 0 1 
_______
**symmetric**
0 1 0 0 
1 0 0 0 
0 0 0 1 
0 0 1 0 
_______
0 1 0 0 
0 0 1 0 
1 0 0 0 
0 0 0 1 
_______
0 1 0 0 
0 0 1 0 
0 0 0 1 
1 0 0 0 
_______
0 1 0 0 
0 0 0 1 
1 0 0 0 
0 0 1 0 
_______
0 1 0 0 
0 0 0 1 
0 0 1 0 
1 0 0 0 
_______
0 0 1 0 
1 0 0 0 
0 1 0 0 
0 0 0 1 
_______
0 0 1 0 
1 0 0 0 
0 0 0 1 
0 1 0 0 
_______
**symmetric**
0 0 1 0 
0 1 0 0 
1 0 0 0 
0 0 0 1 
_______
0 0 1 0 
0 1 0 0 
0 0 0 1 
1 0 0 0 
_______
**symmetric**
0 0 1 0 
0 0 0 1 
1 0 0 0 
0 1 0 0 
_______
0 0 1 0 
0 0 0 1 
0 1 0 0 
1 0 0 0 
_______
0 0 0 1 
1 0 0 0 
0 1 0 0 
0 0 1 0 
_______
0 0 0 1 
1 0 0 0 
0 0 1 0 
0 1 0 0 
_______
0 0 0 1 
0 1 0 0 
1 0 0 0 
0 0 1 0 
_______
**symmetric**
0 0 0 1 
0 1 0 0 
0 0 1 0 
1 0 0 0 
_______
0 0 0 1 
0 0 1 0 
1 0 0 0 
0 1 0 0 
_______
**symmetric**
0 0 0 1 
0 0 1 0 
0 1 0 0 
1 0 0 0 
_______
Number of answers : 24
Number of symmetric answers : 10
___________________________________
behrad@TadavomnisT:~/Desktop$

مساله nرخ - برای n = 4 (باتفاوت):
تابع رو بصورت زیر فراخونی کنید:

n_rooks( 4 , true ); //distinguish between rooks

و خروجی این قسمت :

behrad@TadavomnisT:~/Desktop$ php back_tracking.php 

** 4 ROOKS ** (distinguishing between rooks)
Building empty matrix...
Building decision tree...
Printing decision tree :
.
└── "root"
    ├── [0,0]
    │   ├── [1,1]
    │   │   ├── [2,2]
    │   │   │   └── [3,3]
    │   │   ├── [2,3]
    │   │   │   └── [3,2]
    │   │   ├── [3,2]
    │   │   │   └── [2,3]
    │   │   └── [3,3]
    │   │       └── [2,2]
    │   ├── [1,2]
    │   │   ├── [2,1]
    │   │   │   └── [3,3]
    │   │   ├── [2,3]
    │   │   │   └── [3,1]
    │   │   ├── [3,1]
    │   │   │   └── [2,3]
    │   │   └── [3,3]
    │   │       └── [2,1]
    │   ├── [1,3]
    │   │   ├── [2,1]
    │   │   │   └── [3,2]
    │   │   ├── [2,2]
    │   │   │   └── [3,1]
    │   │   ├── [3,1]
    │   │   │   └── [2,2]
    │   │   └── [3,2]
    │   │       └── [2,1]
    │   ├── [2,1]
    │   │   ├── [1,2]
    │   │   │   └── [3,3]
    │   │   ├── [1,3]
    │   │   │   └── [3,2]
    │   │   ├── [3,2]
    │   │   │   └── [1,3]
    │   │   └── [3,3]
    │   │       └── [1,2]
    │   ├── [2,2]
    │   │   ├── [1,1]
    │   │   │   └── [3,3]
    │   │   ├── [1,3]
    │   │   │   └── [3,1]
    │   │   ├── [3,1]
    │   │   │   └── [1,3]
    │   │   └── [3,3]
    │   │       └── [1,1]
    │   ├── [2,3]
    │   │   ├── [1,1]
    │   │   │   └── [3,2]
    │   │   ├── [1,2]
    │   │   │   └── [3,1]
    │   │   ├── [3,1]
    │   │   │   └── [1,2]
    │   │   └── [3,2]
    │   │       └── [1,1]
    │   ├── [3,1]
    │   │   ├── [1,2]
    │   │   │   └── [2,3]
    │   │   ├── [1,3]
    │   │   │   └── [2,2]
    │   │   ├── [2,2]
    │   │   │   └── [1,3]
    │   │   └── [2,3]
    │   │       └── [1,2]
    │   ├── [3,2]
    │   │   ├── [1,1]
    │   │   │   └── [2,3]
    │   │   ├── [1,3]
    │   │   │   └── [2,1]
    │   │   ├── [2,1]
    │   │   │   └── [1,3]
    │   │   └── [2,3]
    │   │       └── [1,1]
    │   └── [3,3]
    │       ├── [1,1]
    │       │   └── [2,2]
    │       ├── [1,2]
    │       │   └── [2,1]
    │       ├── [2,1]
    │       │   └── [1,2]
    │       └── [2,2]
    │           └── [1,1]
    ├── [0,1]
    │   ├── [1,0]
    │   │   ├── [2,2]
    │   │   │   └── [3,3]
    │   │   ├── [2,3]
    │   │   │   └── [3,2]
    │   │   ├── [3,2]
    │   │   │   └── [2,3]
    │   │   └── [3,3]
    │   │       └── [2,2]
    │   ├── [1,2]
    │   │   ├── [2,0]
    │   │   │   └── [3,3]
    │   │   ├── [2,3]
    │   │   │   └── [3,0]
    │   │   ├── [3,0]
    │   │   │   └── [2,3]
    │   │   └── [3,3]
    │   │       └── [2,0]
    │   ├── [1,3]
    │   │   ├── [2,0]
    │   │   │   └── [3,2]
    │   │   ├── [2,2]
    │   │   │   └── [3,0]
    │   │   ├── [3,0]
    │   │   │   └── [2,2]
    │   │   └── [3,2]
    │   │       └── [2,0]
    │   ├── [2,0]
    │   │   ├── [1,2]
    │   │   │   └── [3,3]
    │   │   ├── [1,3]
    │   │   │   └── [3,2]
    │   │   ├── [3,2]
    │   │   │   └── [1,3]
    │   │   └── [3,3]
    │   │       └── [1,2]
    │   ├── [2,2]
    │   │   ├── [1,0]
    │   │   │   └── [3,3]
    │   │   ├── [1,3]
    │   │   │   └── [3,0]
    │   │   ├── [3,0]
    │   │   │   └── [1,3]
    │   │   └── [3,3]
    │   │       └── [1,0]
    │   ├── [2,3]
    │   │   ├── [1,0]
    │   │   │   └── [3,2]
    │   │   ├── [1,2]
    │   │   │   └── [3,0]
    │   │   ├── [3,0]
    │   │   │   └── [1,2]
    │   │   └── [3,2]
    │   │       └── [1,0]
    │   ├── [3,0]
    │   │   ├── [1,2]
    │   │   │   └── [2,3]
    │   │   ├── [1,3]
    │   │   │   └── [2,2]
    │   │   ├── [2,2]
    │   │   │   └── [1,3]
    │   │   └── [2,3]
    │   │       └── [1,2]
    │   ├── [3,2]
    │   │   ├── [1,0]
    │   │   │   └── [2,3]
    │   │   ├── [1,3]
    │   │   │   └── [2,0]
    │   │   ├── [2,0]
    │   │   │   └── [1,3]
    │   │   └── [2,3]
    │   │       └── [1,0]
    │   └── [3,3]
    │       ├── [1,0]
    │       │   └── [2,2]
    │       ├── [1,2]
    │       │   └── [2,0]
    │       ├── [2,0]
    │       │   └── [1,2]
    │       └── [2,2]
    │           └── [1,0]
    ├── [0,2]
    │   ├── [1,0]
    │   │   ├── [2,1]
    │   │   │   └── [3,3]
    │   │   ├── [2,3]
    │   │   │   └── [3,1]
    │   │   ├── [3,1]
    │   │   │   └── [2,3]
    │   │   └── [3,3]
    │   │       └── [2,1]
    │   ├── [1,1]
    │   │   ├── [2,0]
    │   │   │   └── [3,3]
    │   │   ├── [2,3]
    │   │   │   └── [3,0]
    │   │   ├── [3,0]
    │   │   │   └── [2,3]
    │   │   └── [3,3]
    │   │       └── [2,0]
    │   ├── [1,3]
    │   │   ├── [2,0]
    │   │   │   └── [3,1]
    │   │   ├── [2,1]
    │   │   │   └── [3,0]
    │   │   ├── [3,0]
    │   │   │   └── [2,1]
    │   │   └── [3,1]
    │   │       └── [2,0]
    │   ├── [2,0]
    │   │   ├── [1,1]
    │   │   │   └── [3,3]
    │   │   ├── [1,3]
    │   │   │   └── [3,1]
    │   │   ├── [3,1]
    │   │   │   └── [1,3]
    │   │   └── [3,3]
    │   │       └── [1,1]
    │   ├── [2,1]
    │   │   ├── [1,0]
    │   │   │   └── [3,3]
    │   │   ├── [1,3]
    │   │   │   └── [3,0]
    │   │   ├── [3,0]
    │   │   │   └── [1,3]
    │   │   └── [3,3]
    │   │       └── [1,0]
    │   ├── [2,3]
    │   │   ├── [1,0]
    │   │   │   └── [3,1]
    │   │   ├── [1,1]
    │   │   │   └── [3,0]
    │   │   ├── [3,0]
    │   │   │   └── [1,1]
    │   │   └── [3,1]
    │   │       └── [1,0]
    │   ├── [3,0]
    │   │   ├── [1,1]
    │   │   │   └── [2,3]
    │   │   ├── [1,3]
    │   │   │   └── [2,1]
    │   │   ├── [2,1]
    │   │   │   └── [1,3]
    │   │   └── [2,3]
    │   │       └── [1,1]
    │   ├── [3,1]
    │   │   ├── [1,0]
    │   │   │   └── [2,3]
    │   │   ├── [1,3]
    │   │   │   └── [2,0]
    │   │   ├── [2,0]
    │   │   │   └── [1,3]
    │   │   └── [2,3]
    │   │       └── [1,0]
    │   └── [3,3]
    │       ├── [1,0]
    │       │   └── [2,1]
    │       ├── [1,1]
    │       │   └── [2,0]
    │       ├── [2,0]
    │       │   └── [1,1]
    │       └── [2,1]
    │           └── [1,0]
    ├── [0,3]
    │   ├── [1,0]
    │   │   ├── [2,1]
    │   │   │   └── [3,2]
    │   │   ├── [2,2]
    │   │   │   └── [3,1]
    │   │   ├── [3,1]
    │   │   │   └── [2,2]
    │   │   └── [3,2]
    │   │       └── [2,1]
    │   ├── [1,1]
    │   │   ├── [2,0]
    │   │   │   └── [3,2]
    │   │   ├── [2,2]
    │   │   │   └── [3,0]
    │   │   ├── [3,0]
    │   │   │   └── [2,2]
    │   │   └── [3,2]
    │   │       └── [2,0]
    │   ├── [1,2]
    │   │   ├── [2,0]
    │   │   │   └── [3,1]
    │   │   ├── [2,1]
    │   │   │   └── [3,0]
    │   │   ├── [3,0]
    │   │   │   └── [2,1]
    │   │   └── [3,1]
    │   │       └── [2,0]
    │   ├── [2,0]
    │   │   ├── [1,1]
    │   │   │   └── [3,2]
    │   │   ├── [1,2]
    │   │   │   └── [3,1]
    │   │   ├── [3,1]
    │   │   │   └── [1,2]
    │   │   └── [3,2]
    │   │       └── [1,1]
    │   ├── [2,1]
    │   │   ├── [1,0]
    │   │   │   └── [3,2]
    │   │   ├── [1,2]
    │   │   │   └── [3,0]
    │   │   ├── [3,0]
    │   │   │   └── [1,2]
    │   │   └── [3,2]
    │   │       └── [1,0]
    │   ├── [2,2]
    │   │   ├── [1,0]
    │   │   │   └── [3,1]
    │   │   ├── [1,1]
    │   │   │   └── [3,0]
    │   │   ├── [3,0]
    │   │   │   └── [1,1]
    │   │   └── [3,1]
    │   │       └── [1,0]
    │   ├── [3,0]
    │   │   ├── [1,1]
    │   │   │   └── [2,2]
    │   │   ├── [1,2]
    │   │   │   └── [2,1]
    │   │   ├── [2,1]
    │   │   │   └── [1,2]
    │   │   └── [2,2]
    │   │       └── [1,1]
    │   ├── [3,1]
    │   │   ├── [1,0]
    │   │   │   └── [2,2]
    │   │   ├── [1,2]
    │   │   │   └── [2,0]
    │   │   ├── [2,0]
    │   │   │   └── [1,2]
    │   │   └── [2,2]
    │   │       └── [1,0]
    │   └── [3,2]
    │       ├── [1,0]
    │       │   └── [2,1]
    │       ├── [1,1]
    │       │   └── [2,0]
    │       ├── [2,0]
    │       │   └── [1,1]
    │       └── [2,1]
    │           └── [1,0]
    ├── [1,0]
    │   ├── [0,1]
    │   │   ├── [2,2]
    │   │   │   └── [3,3]
    │   │   ├── [2,3]
    │   │   │   └── [3,2]
    │   │   ├── [3,2]
    │   │   │   └── [2,3]
    │   │   └── [3,3]
    │   │       └── [2,2]
    │   ├── [0,2]
    │   │   ├── [2,1]
    │   │   │   └── [3,3]
    │   │   ├── [2,3]
    │   │   │   └── [3,1]
    │   │   ├── [3,1]
    │   │   │   └── [2,3]
    │   │   └── [3,3]
    │   │       └── [2,1]
    │   ├── [0,3]
    │   │   ├── [2,1]
    │   │   │   └── [3,2]
    │   │   ├── [2,2]
    │   │   │   └── [3,1]
    │   │   ├── [3,1]
    │   │   │   └── [2,2]
    │   │   └── [3,2]
    │   │       └── [2,1]
    │   ├── [2,1]
    │   │   ├── [0,2]
    │   │   │   └── [3,3]
    │   │   ├── [0,3]
    │   │   │   └── [3,2]
    │   │   ├── [3,2]
    │   │   │   └── [0,3]
    │   │   └── [3,3]
    │   │       └── [0,2]
    │   ├── [2,2]
    │   │   ├── [0,1]
    │   │   │   └── [3,3]
    │   │   ├── [0,3]
    │   │   │   └── [3,1]
    │   │   ├── [3,1]
    │   │   │   └── [0,3]
    │   │   └── [3,3]
    │   │       └── [0,1]
    │   ├── [2,3]
    │   │   ├── [0,1]
    │   │   │   └── [3,2]
    │   │   ├── [0,2]
    │   │   │   └── [3,1]
    │   │   ├── [3,1]
    │   │   │   └── [0,2]
    │   │   └── [3,2]
    │   │       └── [0,1]
    │   ├── [3,1]
    │   │   ├── [0,2]
    │   │   │   └── [2,3]
    │   │   ├── [0,3]
    │   │   │   └── [2,2]
    │   │   ├── [2,2]
    │   │   │   └── [0,3]
    │   │   └── [2,3]
    │   │       └── [0,2]
    │   ├── [3,2]
    │   │   ├── [0,1]
    │   │   │   └── [2,3]
    │   │   ├── [0,3]
    │   │   │   └── [2,1]
    │   │   ├── [2,1]
    │   │   │   └── [0,3]
    │   │   └── [2,3]
    │   │       └── [0,1]
    │   └── [3,3]
    │       ├── [0,1]
    │       │   └── [2,2]
    │       ├── [0,2]
    │       │   └── [2,1]
    │       ├── [2,1]
    │       │   └── [0,2]
    │       └── [2,2]
    │           └── [0,1]
    ├── [1,1]
    │   ├── [0,0]
    │   │   ├── [2,2]
    │   │   │   └── [3,3]
    │   │   ├── [2,3]
    │   │   │   └── [3,2]
    │   │   ├── [3,2]
    │   │   │   └── [2,3]
    │   │   └── [3,3]
    │   │       └── [2,2]
    │   ├── [0,2]
    │   │   ├── [2,0]
    │   │   │   └── [3,3]
    │   │   ├── [2,3]
    │   │   │   └── [3,0]
    │   │   ├── [3,0]
    │   │   │   └── [2,3]
    │   │   └── [3,3]
    │   │       └── [2,0]
    │   ├── [0,3]
    │   │   ├── [2,0]
    │   │   │   └── [3,2]
    │   │   ├── [2,2]
    │   │   │   └── [3,0]
    │   │   ├── [3,0]
    │   │   │   └── [2,2]
    │   │   └── [3,2]
    │   │       └── [2,0]
    │   ├── [2,0]
    │   │   ├── [0,2]
    │   │   │   └── [3,3]
    │   │   ├── [0,3]
    │   │   │   └── [3,2]
    │   │   ├── [3,2]
    │   │   │   └── [0,3]
    │   │   └── [3,3]
    │   │       └── [0,2]
    │   ├── [2,2]
    │   │   ├── [0,0]
    │   │   │   └── [3,3]
    │   │   ├── [0,3]
    │   │   │   └── [3,0]
    │   │   ├── [3,0]
    │   │   │   └── [0,3]
    │   │   └── [3,3]
    │   │       └── [0,0]
    │   ├── [2,3]
    │   │   ├── [0,0]
    │   │   │   └── [3,2]
    │   │   ├── [0,2]
    │   │   │   └── [3,0]
    │   │   ├── [3,0]
    │   │   │   └── [0,2]
    │   │   └── [3,2]
    │   │       └── [0,0]
    │   ├── [3,0]
    │   │   ├── [0,2]
    │   │   │   └── [2,3]
    │   │   ├── [0,3]
    │   │   │   └── [2,2]
    │   │   ├── [2,2]
    │   │   │   └── [0,3]
    │   │   └── [2,3]
    │   │       └── [0,2]
    │   ├── [3,2]
    │   │   ├── [0,0]
    │   │   │   └── [2,3]
    │   │   ├── [0,3]
    │   │   │   └── [2,0]
    │   │   ├── [2,0]
    │   │   │   └── [0,3]
    │   │   └── [2,3]
    │   │       └── [0,0]
    │   └── [3,3]
    │       ├── [0,0]
    │       │   └── [2,2]
    │       ├── [0,2]
    │       │   └── [2,0]
    │       ├── [2,0]
    │       │   └── [0,2]
    │       └── [2,2]
    │           └── [0,0]
    ├── [1,2]
    │   ├── [0,0]
    │   │   ├── [2,1]
    │   │   │   └── [3,3]
    │   │   ├── [2,3]
    │   │   │   └── [3,1]
    │   │   ├── [3,1]
    │   │   │   └── [2,3]
    │   │   └── [3,3]
    │   │       └── [2,1]
    │   ├── [0,1]
    │   │   ├── [2,0]
    │   │   │   └── [3,3]
    │   │   ├── [2,3]
    │   │   │   └── [3,0]
    │   │   ├── [3,0]
    │   │   │   └── [2,3]
    │   │   └── [3,3]
    │   │       └── [2,0]
    │   ├── [0,3]
    │   │   ├── [2,0]
    │   │   │   └── [3,1]
    │   │   ├── [2,1]
    │   │   │   └── [3,0]
    │   │   ├── [3,0]
    │   │   │   └── [2,1]
    │   │   └── [3,1]
    │   │       └── [2,0]
    │   ├── [2,0]
    │   │   ├── [0,1]
    │   │   │   └── [3,3]
    │   │   ├── [0,3]
    │   │   │   └── [3,1]
    │   │   ├── [3,1]
    │   │   │   └── [0,3]
    │   │   └── [3,3]
    │   │       └── [0,1]
    │   ├── [2,1]
    │   │   ├── [0,0]
    │   │   │   └── [3,3]
    │   │   ├── [0,3]
    │   │   │   └── [3,0]
    │   │   ├── [3,0]
    │   │   │   └── [0,3]
    │   │   └── [3,3]
    │   │       └── [0,0]
    │   ├── [2,3]
    │   │   ├── [0,0]
    │   │   │   └── [3,1]
    │   │   ├── [0,1]
    │   │   │   └── [3,0]
    │   │   ├── [3,0]
    │   │   │   └── [0,1]
    │   │   └── [3,1]
    │   │       └── [0,0]
    │   ├── [3,0]
    │   │   ├── [0,1]
    │   │   │   └── [2,3]
    │   │   ├── [0,3]
    │   │   │   └── [2,1]
    │   │   ├── [2,1]
    │   │   │   └── [0,3]
    │   │   └── [2,3]
    │   │       └── [0,1]
    │   ├── [3,1]
    │   │   ├── [0,0]
    │   │   │   └── [2,3]
    │   │   ├── [0,3]
    │   │   │   └── [2,0]
    │   │   ├── [2,0]
    │   │   │   └── [0,3]
    │   │   └── [2,3]
    │   │       └── [0,0]
    │   └── [3,3]
    │       ├── [0,0]
    │       │   └── [2,1]
    │       ├── [0,1]
    │       │   └── [2,0]
    │       ├── [2,0]
    │       │   └── [0,1]
    │       └── [2,1]
    │           └── [0,0]
    ├── [1,3]
    │   ├── [0,0]
    │   │   ├── [2,1]
    │   │   │   └── [3,2]
    │   │   ├── [2,2]
    │   │   │   └── [3,1]
    │   │   ├── [3,1]
    │   │   │   └── [2,2]
    │   │   └── [3,2]
    │   │       └── [2,1]
    │   ├── [0,1]
    │   │   ├── [2,0]
    │   │   │   └── [3,2]
    │   │   ├── [2,2]
    │   │   │   └── [3,0]
    │   │   ├── [3,0]
    │   │   │   └── [2,2]
    │   │   └── [3,2]
    │   │       └── [2,0]
    │   ├── [0,2]
    │   │   ├── [2,0]
    │   │   │   └── [3,1]
    │   │   ├── [2,1]
    │   │   │   └── [3,0]
    │   │   ├── [3,0]
    │   │   │   └── [2,1]
    │   │   └── [3,1]
    │   │       └── [2,0]
    │   ├── [2,0]
    │   │   ├── [0,1]
    │   │   │   └── [3,2]
    │   │   ├── [0,2]
    │   │   │   └── [3,1]
    │   │   ├── [3,1]
    │   │   │   └── [0,2]
    │   │   └── [3,2]
    │   │       └── [0,1]
    │   ├── [2,1]
    │   │   ├── [0,0]
    │   │   │   └── [3,2]
    │   │   ├── [0,2]
    │   │   │   └── [3,0]
    │   │   ├── [3,0]
    │   │   │   └── [0,2]
    │   │   └── [3,2]
    │   │       └── [0,0]
    │   ├── [2,2]
    │   │   ├── [0,0]
    │   │   │   └── [3,1]
    │   │   ├── [0,1]
    │   │   │   └── [3,0]
    │   │   ├── [3,0]
    │   │   │   └── [0,1]
    │   │   └── [3,1]
    │   │       └── [0,0]
    │   ├── [3,0]
    │   │   ├── [0,1]
    │   │   │   └── [2,2]
    │   │   ├── [0,2]
    │   │   │   └── [2,1]
    │   │   ├── [2,1]
    │   │   │   └── [0,2]
    │   │   └── [2,2]
    │   │       └── [0,1]
    │   ├── [3,1]
    │   │   ├── [0,0]
    │   │   │   └── [2,2]
    │   │   ├── [0,2]
    │   │   │   └── [2,0]
    │   │   ├── [2,0]
    │   │   │   └── [0,2]
    │   │   └── [2,2]
    │   │       └── [0,0]
    │   └── [3,2]
    │       ├── [0,0]
    │       │   └── [2,1]
    │       ├── [0,1]
    │       │   └── [2,0]
    │       ├── [2,0]
    │       │   └── [0,1]
    │       └── [2,1]
    │           └── [0,0]
    ├── [2,0]
    │   ├── [0,1]
    │   │   ├── [1,2]
    │   │   │   └── [3,3]
    │   │   ├── [1,3]
    │   │   │   └── [3,2]
    │   │   ├── [3,2]
    │   │   │   └── [1,3]
    │   │   └── [3,3]
    │   │       └── [1,2]
    │   ├── [0,2]
    │   │   ├── [1,1]
    │   │   │   └── [3,3]
    │   │   ├── [1,3]
    │   │   │   └── [3,1]
    │   │   ├── [3,1]
    │   │   │   └── [1,3]
    │   │   └── [3,3]
    │   │       └── [1,1]
    │   ├── [0,3]
    │   │   ├── [1,1]
    │   │   │   └── [3,2]
    │   │   ├── [1,2]
    │   │   │   └── [3,1]
    │   │   ├── [3,1]
    │   │   │   └── [1,2]
    │   │   └── [3,2]
    │   │       └── [1,1]
    │   ├── [1,1]
    │   │   ├── [0,2]
    │   │   │   └── [3,3]
    │   │   ├── [0,3]
    │   │   │   └── [3,2]
    │   │   ├── [3,2]
    │   │   │   └── [0,3]
    │   │   └── [3,3]
    │   │       └── [0,2]
    │   ├── [1,2]
    │   │   ├── [0,1]
    │   │   │   └── [3,3]
    │   │   ├── [0,3]
    │   │   │   └── [3,1]
    │   │   ├── [3,1]
    │   │   │   └── [0,3]
    │   │   └── [3,3]
    │   │       └── [0,1]
    │   ├── [1,3]
    │   │   ├── [0,1]
    │   │   │   └── [3,2]
    │   │   ├── [0,2]
    │   │   │   └── [3,1]
    │   │   ├── [3,1]
    │   │   │   └── [0,2]
    │   │   └── [3,2]
    │   │       └── [0,1]
    │   ├── [3,1]
    │   │   ├── [0,2]
    │   │   │   └── [1,3]
    │   │   ├── [0,3]
    │   │   │   └── [1,2]
    │   │   ├── [1,2]
    │   │   │   └── [0,3]
    │   │   └── [1,3]
    │   │       └── [0,2]
    │   ├── [3,2]
    │   │   ├── [0,1]
    │   │   │   └── [1,3]
    │   │   ├── [0,3]
    │   │   │   └── [1,1]
    │   │   ├── [1,1]
    │   │   │   └── [0,3]
    │   │   └── [1,3]
    │   │       └── [0,1]
    │   └── [3,3]
    │       ├── [0,1]
    │       │   └── [1,2]
    │       ├── [0,2]
    │       │   └── [1,1]
    │       ├── [1,1]
    │       │   └── [0,2]
    │       └── [1,2]
    │           └── [0,1]
    ├── [2,1]
    │   ├── [0,0]
    │   │   ├── [1,2]
    │   │   │   └── [3,3]
    │   │   ├── [1,3]
    │   │   │   └── [3,2]
    │   │   ├── [3,2]
    │   │   │   └── [1,3]
    │   │   └── [3,3]
    │   │       └── [1,2]
    │   ├── [0,2]
    │   │   ├── [1,0]
    │   │   │   └── [3,3]
    │   │   ├── [1,3]
    │   │   │   └── [3,0]
    │   │   ├── [3,0]
    │   │   │   └── [1,3]
    │   │   └── [3,3]
    │   │       └── [1,0]
    │   ├── [0,3]
    │   │   ├── [1,0]
    │   │   │   └── [3,2]
    │   │   ├── [1,2]
    │   │   │   └── [3,0]
    │   │   ├── [3,0]
    │   │   │   └── [1,2]
    │   │   └── [3,2]
    │   │       └── [1,0]
    │   ├── [1,0]
    │   │   ├── [0,2]
    │   │   │   └── [3,3]
    │   │   ├── [0,3]
    │   │   │   └── [3,2]
    │   │   ├── [3,2]
    │   │   │   └── [0,3]
    │   │   └── [3,3]
    │   │       └── [0,2]
    │   ├── [1,2]
    │   │   ├── [0,0]
    │   │   │   └── [3,3]
    │   │   ├── [0,3]
    │   │   │   └── [3,0]
    │   │   ├── [3,0]
    │   │   │   └── [0,3]
    │   │   └── [3,3]
    │   │       └── [0,0]
    │   ├── [1,3]
    │   │   ├── [0,0]
    │   │   │   └── [3,2]
    │   │   ├── [0,2]
    │   │   │   └── [3,0]
    │   │   ├── [3,0]
    │   │   │   └── [0,2]
    │   │   └── [3,2]
    │   │       └── [0,0]
    │   ├── [3,0]
    │   │   ├── [0,2]
    │   │   │   └── [1,3]
    │   │   ├── [0,3]
    │   │   │   └── [1,2]
    │   │   ├── [1,2]
    │   │   │   └── [0,3]
    │   │   └── [1,3]
    │   │       └── [0,2]
    │   ├── [3,2]
    │   │   ├── [0,0]
    │   │   │   └── [1,3]
    │   │   ├── [0,3]
    │   │   │   └── [1,0]
    │   │   ├── [1,0]
    │   │   │   └── [0,3]
    │   │   └── [1,3]
    │   │       └── [0,0]
    │   └── [3,3]
    │       ├── [0,0]
    │       │   └── [1,2]
    │       ├── [0,2]
    │       │   └── [1,0]
    │       ├── [1,0]
    │       │   └── [0,2]
    │       └── [1,2]
    │           └── [0,0]
    ├── [2,2]
    │   ├── [0,0]
    │   │   ├── [1,1]
    │   │   │   └── [3,3]
    │   │   ├── [1,3]
    │   │   │   └── [3,1]
    │   │   ├── [3,1]
    │   │   │   └── [1,3]
    │   │   └── [3,3]
    │   │       └── [1,1]
    │   ├── [0,1]
    │   │   ├── [1,0]
    │   │   │   └── [3,3]
    │   │   ├── [1,3]
    │   │   │   └── [3,0]
    │   │   ├── [3,0]
    │   │   │   └── [1,3]
    │   │   └── [3,3]
    │   │       └── [1,0]
    │   ├── [0,3]
    │   │   ├── [1,0]
    │   │   │   └── [3,1]
    │   │   ├── [1,1]
    │   │   │   └── [3,0]
    │   │   ├── [3,0]
    │   │   │   └── [1,1]
    │   │   └── [3,1]
    │   │       └── [1,0]
    │   ├── [1,0]
    │   │   ├── [0,1]
    │   │   │   └── [3,3]
    │   │   ├── [0,3]
    │   │   │   └── [3,1]
    │   │   ├── [3,1]
    │   │   │   └── [0,3]
    │   │   └── [3,3]
    │   │       └── [0,1]
    │   ├── [1,1]
    │   │   ├── [0,0]
    │   │   │   └── [3,3]
    │   │   ├── [0,3]
    │   │   │   └── [3,0]
    │   │   ├── [3,0]
    │   │   │   └── [0,3]
    │   │   └── [3,3]
    │   │       └── [0,0]
    │   ├── [1,3]
    │   │   ├── [0,0]
    │   │   │   └── [3,1]
    │   │   ├── [0,1]
    │   │   │   └── [3,0]
    │   │   ├── [3,0]
    │   │   │   └── [0,1]
    │   │   └── [3,1]
    │   │       └── [0,0]
    │   ├── [3,0]
    │   │   ├── [0,1]
    │   │   │   └── [1,3]
    │   │   ├── [0,3]
    │   │   │   └── [1,1]
    │   │   ├── [1,1]
    │   │   │   └── [0,3]
    │   │   └── [1,3]
    │   │       └── [0,1]
    │   ├── [3,1]
    │   │   ├── [0,0]
    │   │   │   └── [1,3]
    │   │   ├── [0,3]
    │   │   │   └── [1,0]
    │   │   ├── [1,0]
    │   │   │   └── [0,3]
    │   │   └── [1,3]
    │   │       └── [0,0]
    │   └── [3,3]
    │       ├── [0,0]
    │       │   └── [1,1]
    │       ├── [0,1]
    │       │   └── [1,0]
    │       ├── [1,0]
    │       │   └── [0,1]
    │       └── [1,1]
    │           └── [0,0]
    ├── [2,3]
    │   ├── [0,0]
    │   │   ├── [1,1]
    │   │   │   └── [3,2]
    │   │   ├── [1,2]
    │   │   │   └── [3,1]
    │   │   ├── [3,1]
    │   │   │   └── [1,2]
    │   │   └── [3,2]
    │   │       └── [1,1]
    │   ├── [0,1]
    │   │   ├── [1,0]
    │   │   │   └── [3,2]
    │   │   ├── [1,2]
    │   │   │   └── [3,0]
    │   │   ├── [3,0]
    │   │   │   └── [1,2]
    │   │   └── [3,2]
    │   │       └── [1,0]
    │   ├── [0,2]
    │   │   ├── [1,0]
    │   │   │   └── [3,1]
    │   │   ├── [1,1]
    │   │   │   └── [3,0]
    │   │   ├── [3,0]
    │   │   │   └── [1,1]
    │   │   └── [3,1]
    │   │       └── [1,0]
    │   ├── [1,0]
    │   │   ├── [0,1]
    │   │   │   └── [3,2]
    │   │   ├── [0,2]
    │   │   │   └── [3,1]
    │   │   ├── [3,1]
    │   │   │   └── [0,2]
    │   │   └── [3,2]
    │   │       └── [0,1]
    │   ├── [1,1]
    │   │   ├── [0,0]
    │   │   │   └── [3,2]
    │   │   ├── [0,2]
    │   │   │   └── [3,0]
    │   │   ├── [3,0]
    │   │   │   └── [0,2]
    │   │   └── [3,2]
    │   │       └── [0,0]
    │   ├── [1,2]
    │   │   ├── [0,0]
    │   │   │   └── [3,1]
    │   │   ├── [0,1]
    │   │   │   └── [3,0]
    │   │   ├── [3,0]
    │   │   │   └── [0,1]
    │   │   └── [3,1]
    │   │       └── [0,0]
    │   ├── [3,0]
    │   │   ├── [0,1]
    │   │   │   └── [1,2]
    │   │   ├── [0,2]
    │   │   │   └── [1,1]
    │   │   ├── [1,1]
    │   │   │   └── [0,2]
    │   │   └── [1,2]
    │   │       └── [0,1]
    │   ├── [3,1]
    │   │   ├── [0,0]
    │   │   │   └── [1,2]
    │   │   ├── [0,2]
    │   │   │   └── [1,0]
    │   │   ├── [1,0]
    │   │   │   └── [0,2]
    │   │   └── [1,2]
    │   │       └── [0,0]
    │   └── [3,2]
    │       ├── [0,0]
    │       │   └── [1,1]
    │       ├── [0,1]
    │       │   └── [1,0]
    │       ├── [1,0]
    │       │   └── [0,1]
    │       └── [1,1]
    │           └── [0,0]
    ├── [3,0]
    │   ├── [0,1]
    │   │   ├── [1,2]
    │   │   │   └── [2,3]
    │   │   ├── [1,3]
    │   │   │   └── [2,2]
    │   │   ├── [2,2]
    │   │   │   └── [1,3]
    │   │   └── [2,3]
    │   │       └── [1,2]
    │   ├── [0,2]
    │   │   ├── [1,1]
    │   │   │   └── [2,3]
    │   │   ├── [1,3]
    │   │   │   └── [2,1]
    │   │   ├── [2,1]
    │   │   │   └── [1,3]
    │   │   └── [2,3]
    │   │       └── [1,1]
    │   ├── [0,3]
    │   │   ├── [1,1]
    │   │   │   └── [2,2]
    │   │   ├── [1,2]
    │   │   │   └── [2,1]
    │   │   ├── [2,1]
    │   │   │   └── [1,2]
    │   │   └── [2,2]
    │   │       └── [1,1]
    │   ├── [1,1]
    │   │   ├── [0,2]
    │   │   │   └── [2,3]
    │   │   ├── [0,3]
    │   │   │   └── [2,2]
    │   │   ├── [2,2]
    │   │   │   └── [0,3]
    │   │   └── [2,3]
    │   │       └── [0,2]
    │   ├── [1,2]
    │   │   ├── [0,1]
    │   │   │   └── [2,3]
    │   │   ├── [0,3]
    │   │   │   └── [2,1]
    │   │   ├── [2,1]
    │   │   │   └── [0,3]
    │   │   └── [2,3]
    │   │       └── [0,1]
    │   ├── [1,3]
    │   │   ├── [0,1]
    │   │   │   └── [2,2]
    │   │   ├── [0,2]
    │   │   │   └── [2,1]
    │   │   ├── [2,1]
    │   │   │   └── [0,2]
    │   │   └── [2,2]
    │   │       └── [0,1]
    │   ├── [2,1]
    │   │   ├── [0,2]
    │   │   │   └── [1,3]
    │   │   ├── [0,3]
    │   │   │   └── [1,2]
    │   │   ├── [1,2]
    │   │   │   └── [0,3]
    │   │   └── [1,3]
    │   │       └── [0,2]
    │   ├── [2,2]
    │   │   ├── [0,1]
    │   │   │   └── [1,3]
    │   │   ├── [0,3]
    │   │   │   └── [1,1]
    │   │   ├── [1,1]
    │   │   │   └── [0,3]
    │   │   └── [1,3]
    │   │       └── [0,1]
    │   └── [2,3]
    │       ├── [0,1]
    │       │   └── [1,2]
    │       ├── [0,2]
    │       │   └── [1,1]
    │       ├── [1,1]
    │       │   └── [0,2]
    │       └── [1,2]
    │           └── [0,1]
    ├── [3,1]
    │   ├── [0,0]
    │   │   ├── [1,2]
    │   │   │   └── [2,3]
    │   │   ├── [1,3]
    │   │   │   └── [2,2]
    │   │   ├── [2,2]
    │   │   │   └── [1,3]
    │   │   └── [2,3]
    │   │       └── [1,2]
    │   ├── [0,2]
    │   │   ├── [1,0]
    │   │   │   └── [2,3]
    │   │   ├── [1,3]
    │   │   │   └── [2,0]
    │   │   ├── [2,0]
    │   │   │   └── [1,3]
    │   │   └── [2,3]
    │   │       └── [1,0]
    │   ├── [0,3]
    │   │   ├── [1,0]
    │   │   │   └── [2,2]
    │   │   ├── [1,2]
    │   │   │   └── [2,0]
    │   │   ├── [2,0]
    │   │   │   └── [1,2]
    │   │   └── [2,2]
    │   │       └── [1,0]
    │   ├── [1,0]
    │   │   ├── [0,2]
    │   │   │   └── [2,3]
    │   │   ├── [0,3]
    │   │   │   └── [2,2]
    │   │   ├── [2,2]
    │   │   │   └── [0,3]
    │   │   └── [2,3]
    │   │       └── [0,2]
    │   ├── [1,2]
    │   │   ├── [0,0]
    │   │   │   └── [2,3]
    │   │   ├── [0,3]
    │   │   │   └── [2,0]
    │   │   ├── [2,0]
    │   │   │   └── [0,3]
    │   │   └── [2,3]
    │   │       └── [0,0]
    │   ├── [1,3]
    │   │   ├── [0,0]
    │   │   │   └── [2,2]
    │   │   ├── [0,2]
    │   │   │   └── [2,0]
    │   │   ├── [2,0]
    │   │   │   └── [0,2]
    │   │   └── [2,2]
    │   │       └── [0,0]
    │   ├── [2,0]
    │   │   ├── [0,2]
    │   │   │   └── [1,3]
    │   │   ├── [0,3]
    │   │   │   └── [1,2]
    │   │   ├── [1,2]
    │   │   │   └── [0,3]
    │   │   └── [1,3]
    │   │       └── [0,2]
    │   ├── [2,2]
    │   │   ├── [0,0]
    │   │   │   └── [1,3]
    │   │   ├── [0,3]
    │   │   │   └── [1,0]
    │   │   ├── [1,0]
    │   │   │   └── [0,3]
    │   │   └── [1,3]
    │   │       └── [0,0]
    │   └── [2,3]
    │       ├── [0,0]
    │       │   └── [1,2]
    │       ├── [0,2]
    │       │   └── [1,0]
    │       ├── [1,0]
    │       │   └── [0,2]
    │       └── [1,2]
    │           └── [0,0]
    ├── [3,2]
    │   ├── [0,0]
    │   │   ├── [1,1]
    │   │   │   └── [2,3]
    │   │   ├── [1,3]
    │   │   │   └── [2,1]
    │   │   ├── [2,1]
    │   │   │   └── [1,3]
    │   │   └── [2,3]
    │   │       └── [1,1]
    │   ├── [0,1]
    │   │   ├── [1,0]
    │   │   │   └── [2,3]
    │   │   ├── [1,3]
    │   │   │   └── [2,0]
    │   │   ├── [2,0]
    │   │   │   └── [1,3]
    │   │   └── [2,3]
    │   │       └── [1,0]
    │   ├── [0,3]
    │   │   ├── [1,0]
    │   │   │   └── [2,1]
    │   │   ├── [1,1]
    │   │   │   └── [2,0]
    │   │   ├── [2,0]
    │   │   │   └── [1,1]
    │   │   └── [2,1]
    │   │       └── [1,0]
    │   ├── [1,0]
    │   │   ├── [0,1]
    │   │   │   └── [2,3]
    │   │   ├── [0,3]
    │   │   │   └── [2,1]
    │   │   ├── [2,1]
    │   │   │   └── [0,3]
    │   │   └── [2,3]
    │   │       └── [0,1]
    │   ├── [1,1]
    │   │   ├── [0,0]
    │   │   │   └── [2,3]
    │   │   ├── [0,3]
    │   │   │   └── [2,0]
    │   │   ├── [2,0]
    │   │   │   └── [0,3]
    │   │   └── [2,3]
    │   │       └── [0,0]
    │   ├── [1,3]
    │   │   ├── [0,0]
    │   │   │   └── [2,1]
    │   │   ├── [0,1]
    │   │   │   └── [2,0]
    │   │   ├── [2,0]
    │   │   │   └── [0,1]
    │   │   └── [2,1]
    │   │       └── [0,0]
    │   ├── [2,0]
    │   │   ├── [0,1]
    │   │   │   └── [1,3]
    │   │   ├── [0,3]
    │   │   │   └── [1,1]
    │   │   ├── [1,1]
    │   │   │   └── [0,3]
    │   │   └── [1,3]
    │   │       └── [0,1]
    │   ├── [2,1]
    │   │   ├── [0,0]
    │   │   │   └── [1,3]
    │   │   ├── [0,3]
    │   │   │   └── [1,0]
    │   │   ├── [1,0]
    │   │   │   └── [0,3]
    │   │   └── [1,3]
    │   │       └── [0,0]
    │   └── [2,3]
    │       ├── [0,0]
    │       │   └── [1,1]
    │       ├── [0,1]
    │       │   └── [1,0]
    │       ├── [1,0]
    │       │   └── [0,1]
    │       └── [1,1]
    │           └── [0,0]
    └── [3,3]
        ├── [0,0]
        │   ├── [1,1]
        │   │   └── [2,2]
        │   ├── [1,2]
        │   │   └── [2,1]
        │   ├── [2,1]
        │   │   └── [1,2]
        │   └── [2,2]
        │       └── [1,1]
        ├── [0,1]
        │   ├── [1,0]
        │   │   └── [2,2]
        │   ├── [1,2]
        │   │   └── [2,0]
        │   ├── [2,0]
        │   │   └── [1,2]
        │   └── [2,2]
        │       └── [1,0]
        ├── [0,2]
        │   ├── [1,0]
        │   │   └── [2,1]
        │   ├── [1,1]
        │   │   └── [2,0]
        │   ├── [2,0]
        │   │   └── [1,1]
        │   └── [2,1]
        │       └── [1,0]
        ├── [1,0]
        │   ├── [0,1]
        │   │   └── [2,2]
        │   ├── [0,2]
        │   │   └── [2,1]
        │   ├── [2,1]
        │   │   └── [0,2]
        │   └── [2,2]
        │       └── [0,1]
        ├── [1,1]
        │   ├── [0,0]
        │   │   └── [2,2]
        │   ├── [0,2]
        │   │   └── [2,0]
        │   ├── [2,0]
        │   │   └── [0,2]
        │   └── [2,2]
        │       └── [0,0]
        ├── [1,2]
        │   ├── [0,0]
        │   │   └── [2,1]
        │   ├── [0,1]
        │   │   └── [2,0]
        │   ├── [2,0]
        │   │   └── [0,1]
        │   └── [2,1]
        │       └── [0,0]
        ├── [2,0]
        │   ├── [0,1]
        │   │   └── [1,2]
        │   ├── [0,2]
        │   │   └── [1,1]
        │   ├── [1,1]
        │   │   └── [0,2]
        │   └── [1,2]
        │       └── [0,1]
        ├── [2,1]
        │   ├── [0,0]
        │   │   └── [1,2]
        │   ├── [0,2]
        │   │   └── [1,0]
        │   ├── [1,0]
        │   │   └── [0,2]
        │   └── [1,2]
        │       └── [0,0]
        └── [2,2]
            ├── [0,0]
            │   └── [1,1]
            ├── [0,1]
            │   └── [1,0]
            ├── [1,0]
            │   └── [0,1]
            └── [1,1]
                └── [0,0]

Printing all possible solutions :
1 0 0 0 
0 2 0 0 
0 0 3 0 
0 0 0 4 
_______
1 0 0 0 
0 2 0 0 
0 0 0 3 
0 0 4 0 
_______
1 0 0 0 
0 2 0 0 
0 0 0 4 
0 0 3 0 
_______
1 0 0 0 
0 2 0 0 
0 0 4 0 
0 0 0 3 
_______
1 0 0 0 
0 0 2 0 
0 3 0 0 
0 0 0 4 
_______
1 0 0 0 
0 0 2 0 
0 0 0 3 
0 4 0 0 
_______
1 0 0 0 
0 0 2 0 
0 0 0 4 
0 3 0 0 
_______
1 0 0 0 
0 0 2 0 
0 4 0 0 
0 0 0 3 
_______
1 0 0 0 
0 0 0 2 
0 3 0 0 
0 0 4 0 
_______
1 0 0 0 
0 0 0 2 
0 0 3 0 
0 4 0 0 
_______
1 0 0 0 
0 0 0 2 
0 0 4 0 
0 3 0 0 
_______
1 0 0 0 
0 0 0 2 
0 4 0 0 
0 0 3 0 
_______
1 0 0 0 
0 0 3 0 
0 2 0 0 
0 0 0 4 
_______
1 0 0 0 
0 0 0 3 
0 2 0 0 
0 0 4 0 
_______
1 0 0 0 
0 0 0 4 
0 2 0 0 
0 0 3 0 
_______
1 0 0 0 
0 0 4 0 
0 2 0 0 
0 0 0 3 
_______
1 0 0 0 
0 3 0 0 
0 0 2 0 
0 0 0 4 
_______
1 0 0 0 
0 0 0 3 
0 0 2 0 
0 4 0 0 
_______
1 0 0 0 
0 0 0 4 
0 0 2 0 
0 3 0 0 
_______
1 0 0 0 
0 4 0 0 
0 0 2 0 
0 0 0 3 
_______
1 0 0 0 
0 3 0 0 
0 0 0 2 
0 0 4 0 
_______
1 0 0 0 
0 0 3 0 
0 0 0 2 
0 4 0 0 
_______
1 0 0 0 
0 0 4 0 
0 0 0 2 
0 3 0 0 
_______
1 0 0 0 
0 4 0 0 
0 0 0 2 
0 0 3 0 
_______
1 0 0 0 
0 0 3 0 
0 0 0 4 
0 2 0 0 
_______
1 0 0 0 
0 0 0 3 
0 0 4 0 
0 2 0 0 
_______
1 0 0 0 
0 0 0 4 
0 0 3 0 
0 2 0 0 
_______
1 0 0 0 
0 0 4 0 
0 0 0 3 
0 2 0 0 
_______
1 0 0 0 
0 3 0 0 
0 0 0 4 
0 0 2 0 
_______
1 0 0 0 
0 0 0 3 
0 4 0 0 
0 0 2 0 
_______
1 0 0 0 
0 0 0 4 
0 3 0 0 
0 0 2 0 
_______
1 0 0 0 
0 4 0 0 
0 0 0 3 
0 0 2 0 
_______
1 0 0 0 
0 3 0 0 
0 0 4 0 
0 0 0 2 
_______
1 0 0 0 
0 0 3 0 
0 4 0 0 
0 0 0 2 
_______
1 0 0 0 
0 0 4 0 
0 3 0 0 
0 0 0 2 
_______
1 0 0 0 
0 4 0 0 
0 0 3 0 
0 0 0 2 
_______
0 1 0 0 
2 0 0 0 
0 0 3 0 
0 0 0 4 
_______
0 1 0 0 
2 0 0 0 
0 0 0 3 
0 0 4 0 
_______
0 1 0 0 
2 0 0 0 
0 0 0 4 
0 0 3 0 
_______
0 1 0 0 
2 0 0 0 
0 0 4 0 
0 0 0 3 
_______
0 1 0 0 
0 0 2 0 
3 0 0 0 
0 0 0 4 
_______
0 1 0 0 
0 0 2 0 
0 0 0 3 
4 0 0 0 
_______
0 1 0 0 
0 0 2 0 
0 0 0 4 
3 0 0 0 
_______
0 1 0 0 
0 0 2 0 
4 0 0 0 
0 0 0 3 
_______
0 1 0 0 
0 0 0 2 
3 0 0 0 
0 0 4 0 
_______
0 1 0 0 
0 0 0 2 
0 0 3 0 
4 0 0 0 
_______
0 1 0 0 
0 0 0 2 
0 0 4 0 
3 0 0 0 
_______
0 1 0 0 
0 0 0 2 
4 0 0 0 
0 0 3 0 
_______
0 1 0 0 
0 0 3 0 
2 0 0 0 
0 0 0 4 
_______
0 1 0 0 
0 0 0 3 
2 0 0 0 
0 0 4 0 
_______
0 1 0 0 
0 0 0 4 
2 0 0 0 
0 0 3 0 
_______
0 1 0 0 
0 0 4 0 
2 0 0 0 
0 0 0 3 
_______
0 1 0 0 
3 0 0 0 
0 0 2 0 
0 0 0 4 
_______
0 1 0 0 
0 0 0 3 
0 0 2 0 
4 0 0 0 
_______
0 1 0 0 
0 0 0 4 
0 0 2 0 
3 0 0 0 
_______
0 1 0 0 
4 0 0 0 
0 0 2 0 
0 0 0 3 
_______
0 1 0 0 
3 0 0 0 
0 0 0 2 
0 0 4 0 
_______
0 1 0 0 
0 0 3 0 
0 0 0 2 
4 0 0 0 
_______
0 1 0 0 
0 0 4 0 
0 0 0 2 
3 0 0 0 
_______
0 1 0 0 
4 0 0 0 
0 0 0 2 
0 0 3 0 
_______
0 1 0 0 
0 0 3 0 
0 0 0 4 
2 0 0 0 
_______
0 1 0 0 
0 0 0 3 
0 0 4 0 
2 0 0 0 
_______
0 1 0 0 
0 0 0 4 
0 0 3 0 
2 0 0 0 
_______
0 1 0 0 
0 0 4 0 
0 0 0 3 
2 0 0 0 
_______
0 1 0 0 
3 0 0 0 
0 0 0 4 
0 0 2 0 
_______
0 1 0 0 
0 0 0 3 
4 0 0 0 
0 0 2 0 
_______
0 1 0 0 
0 0 0 4 
3 0 0 0 
0 0 2 0 
_______
0 1 0 0 
4 0 0 0 
0 0 0 3 
0 0 2 0 
_______
0 1 0 0 
3 0 0 0 
0 0 4 0 
0 0 0 2 
_______
0 1 0 0 
0 0 3 0 
4 0 0 0 
0 0 0 2 
_______
0 1 0 0 
0 0 4 0 
3 0 0 0 
0 0 0 2 
_______
0 1 0 0 
4 0 0 0 
0 0 3 0 
0 0 0 2 
_______
0 0 1 0 
2 0 0 0 
0 3 0 0 
0 0 0 4 
_______
0 0 1 0 
2 0 0 0 
0 0 0 3 
0 4 0 0 
_______
0 0 1 0 
2 0 0 0 
0 0 0 4 
0 3 0 0 
_______
0 0 1 0 
2 0 0 0 
0 4 0 0 
0 0 0 3 
_______
0 0 1 0 
0 2 0 0 
3 0 0 0 
0 0 0 4 
_______
0 0 1 0 
0 2 0 0 
0 0 0 3 
4 0 0 0 
_______
0 0 1 0 
0 2 0 0 
0 0 0 4 
3 0 0 0 
_______
0 0 1 0 
0 2 0 0 
4 0 0 0 
0 0 0 3 
_______
0 0 1 0 
0 0 0 2 
3 0 0 0 
0 4 0 0 
_______
0 0 1 0 
0 0 0 2 
0 3 0 0 
4 0 0 0 
_______
0 0 1 0 
0 0 0 2 
0 4 0 0 
3 0 0 0 
_______
0 0 1 0 
0 0 0 2 
4 0 0 0 
0 3 0 0 
_______
0 0 1 0 
0 3 0 0 
2 0 0 0 
0 0 0 4 
_______
0 0 1 0 
0 0 0 3 
2 0 0 0 
0 4 0 0 
_______
0 0 1 0 
0 0 0 4 
2 0 0 0 
0 3 0 0 
_______
0 0 1 0 
0 4 0 0 
2 0 0 0 
0 0 0 3 
_______
0 0 1 0 
3 0 0 0 
0 2 0 0 
0 0 0 4 
_______
0 0 1 0 
0 0 0 3 
0 2 0 0 
4 0 0 0 
_______
0 0 1 0 
0 0 0 4 
0 2 0 0 
3 0 0 0 
_______
0 0 1 0 
4 0 0 0 
0 2 0 0 
0 0 0 3 
_______
0 0 1 0 
3 0 0 0 
0 0 0 2 
0 4 0 0 
_______
0 0 1 0 
0 3 0 0 
0 0 0 2 
4 0 0 0 
_______
0 0 1 0 
0 4 0 0 
0 0 0 2 
3 0 0 0 
_______
0 0 1 0 
4 0 0 0 
0 0 0 2 
0 3 0 0 
_______
0 0 1 0 
0 3 0 0 
0 0 0 4 
2 0 0 0 
_______
0 0 1 0 
0 0 0 3 
0 4 0 0 
2 0 0 0 
_______
0 0 1 0 
0 0 0 4 
0 3 0 0 
2 0 0 0 
_______
0 0 1 0 
0 4 0 0 
0 0 0 3 
2 0 0 0 
_______
0 0 1 0 
3 0 0 0 
0 0 0 4 
0 2 0 0 
_______
0 0 1 0 
0 0 0 3 
4 0 0 0 
0 2 0 0 
_______
0 0 1 0 
0 0 0 4 
3 0 0 0 
0 2 0 0 
_______
0 0 1 0 
4 0 0 0 
0 0 0 3 
0 2 0 0 
_______
0 0 1 0 
3 0 0 0 
0 4 0 0 
0 0 0 2 
_______
0 0 1 0 
0 3 0 0 
4 0 0 0 
0 0 0 2 
_______
0 0 1 0 
0 4 0 0 
3 0 0 0 
0 0 0 2 
_______
0 0 1 0 
4 0 0 0 
0 3 0 0 
0 0 0 2 
_______
0 0 0 1 
2 0 0 0 
0 3 0 0 
0 0 4 0 
_______
0 0 0 1 
2 0 0 0 
0 0 3 0 
0 4 0 0 
_______
0 0 0 1 
2 0 0 0 
0 0 4 0 
0 3 0 0 
_______
0 0 0 1 
2 0 0 0 
0 4 0 0 
0 0 3 0 
_______
0 0 0 1 
0 2 0 0 
3 0 0 0 
0 0 4 0 
_______
0 0 0 1 
0 2 0 0 
0 0 3 0 
4 0 0 0 
_______
0 0 0 1 
0 2 0 0 
0 0 4 0 
3 0 0 0 
_______
0 0 0 1 
0 2 0 0 
4 0 0 0 
0 0 3 0 
_______
0 0 0 1 
0 0 2 0 
3 0 0 0 
0 4 0 0 
_______
0 0 0 1 
0 0 2 0 
0 3 0 0 
4 0 0 0 
_______
0 0 0 1 
0 0 2 0 
0 4 0 0 
3 0 0 0 
_______
0 0 0 1 
0 0 2 0 
4 0 0 0 
0 3 0 0 
_______
0 0 0 1 
0 3 0 0 
2 0 0 0 
0 0 4 0 
_______
0 0 0 1 
0 0 3 0 
2 0 0 0 
0 4 0 0 
_______
0 0 0 1 
0 0 4 0 
2 0 0 0 
0 3 0 0 
_______
0 0 0 1 
0 4 0 0 
2 0 0 0 
0 0 3 0 
_______
0 0 0 1 
3 0 0 0 
0 2 0 0 
0 0 4 0 
_______
0 0 0 1 
0 0 3 0 
0 2 0 0 
4 0 0 0 
_______
0 0 0 1 
0 0 4 0 
0 2 0 0 
3 0 0 0 
_______
0 0 0 1 
4 0 0 0 
0 2 0 0 
0 0 3 0 
_______
0 0 0 1 
3 0 0 0 
0 0 2 0 
0 4 0 0 
_______
0 0 0 1 
0 3 0 0 
0 0 2 0 
4 0 0 0 
_______
0 0 0 1 
0 4 0 0 
0 0 2 0 
3 0 0 0 
_______
0 0 0 1 
4 0 0 0 
0 0 2 0 
0 3 0 0 
_______
0 0 0 1 
0 3 0 0 
0 0 4 0 
2 0 0 0 
_______
0 0 0 1 
0 0 3 0 
0 4 0 0 
2 0 0 0 
_______
0 0 0 1 
0 0 4 0 
0 3 0 0 
2 0 0 0 
_______
0 0 0 1 
0 4 0 0 
0 0 3 0 
2 0 0 0 
_______
0 0 0 1 
3 0 0 0 
0 0 4 0 
0 2 0 0 
_______
0 0 0 1 
0 0 3 0 
4 0 0 0 
0 2 0 0 
_______
0 0 0 1 
0 0 4 0 
3 0 0 0 
0 2 0 0 
_______
0 0 0 1 
4 0 0 0 
0 0 3 0 
0 2 0 0 
_______
0 0 0 1 
3 0 0 0 
0 4 0 0 
0 0 2 0 
_______
0 0 0 1 
0 3 0 0 
4 0 0 0 
0 0 2 0 
_______
0 0 0 1 
0 4 0 0 
3 0 0 0 
0 0 2 0 
_______
0 0 0 1 
4 0 0 0 
0 3 0 0 
0 0 2 0 
_______
0 2 0 0 
1 0 0 0 
0 0 3 0 
0 0 0 4 
_______
0 2 0 0 
1 0 0 0 
0 0 0 3 
0 0 4 0 
_______
0 2 0 0 
1 0 0 0 
0 0 0 4 
0 0 3 0 
_______
0 2 0 0 
1 0 0 0 
0 0 4 0 
0 0 0 3 
_______
0 0 2 0 
1 0 0 0 
0 3 0 0 
0 0 0 4 
_______
0 0 2 0 
1 0 0 0 
0 0 0 3 
0 4 0 0 
_______
0 0 2 0 
1 0 0 0 
0 0 0 4 
0 3 0 0 
_______
0 0 2 0 
1 0 0 0 
0 4 0 0 
0 0 0 3 
_______
0 0 0 2 
1 0 0 0 
0 3 0 0 
0 0 4 0 
_______
0 0 0 2 
1 0 0 0 
0 0 3 0 
0 4 0 0 
_______
0 0 0 2 
1 0 0 0 
0 0 4 0 
0 3 0 0 
_______
0 0 0 2 
1 0 0 0 
0 4 0 0 
0 0 3 0 
_______
0 0 3 0 
1 0 0 0 
0 2 0 0 
0 0 0 4 
_______
0 0 0 3 
1 0 0 0 
0 2 0 0 
0 0 4 0 
_______
0 0 0 4 
1 0 0 0 
0 2 0 0 
0 0 3 0 
_______
0 0 4 0 
1 0 0 0 
0 2 0 0 
0 0 0 3 
_______
0 3 0 0 
1 0 0 0 
0 0 2 0 
0 0 0 4 
_______
0 0 0 3 
1 0 0 0 
0 0 2 0 
0 4 0 0 
_______
0 0 0 4 
1 0 0 0 
0 0 2 0 
0 3 0 0 
_______
0 4 0 0 
1 0 0 0 
0 0 2 0 
0 0 0 3 
_______
0 3 0 0 
1 0 0 0 
0 0 0 2 
0 0 4 0 
_______
0 0 3 0 
1 0 0 0 
0 0 0 2 
0 4 0 0 
_______
0 0 4 0 
1 0 0 0 
0 0 0 2 
0 3 0 0 
_______
0 4 0 0 
1 0 0 0 
0 0 0 2 
0 0 3 0 
_______
0 0 3 0 
1 0 0 0 
0 0 0 4 
0 2 0 0 
_______
0 0 0 3 
1 0 0 0 
0 0 4 0 
0 2 0 0 
_______
0 0 0 4 
1 0 0 0 
0 0 3 0 
0 2 0 0 
_______
0 0 4 0 
1 0 0 0 
0 0 0 3 
0 2 0 0 
_______
0 3 0 0 
1 0 0 0 
0 0 0 4 
0 0 2 0 
_______
0 0 0 3 
1 0 0 0 
0 4 0 0 
0 0 2 0 
_______
0 0 0 4 
1 0 0 0 
0 3 0 0 
0 0 2 0 
_______
0 4 0 0 
1 0 0 0 
0 0 0 3 
0 0 2 0 
_______
0 3 0 0 
1 0 0 0 
0 0 4 0 
0 0 0 2 
_______
0 0 3 0 
1 0 0 0 
0 4 0 0 
0 0 0 2 
_______
0 0 4 0 
1 0 0 0 
0 3 0 0 
0 0 0 2 
_______
0 4 0 0 
1 0 0 0 
0 0 3 0 
0 0 0 2 
_______
2 0 0 0 
0 1 0 0 
0 0 3 0 
0 0 0 4 
_______
2 0 0 0 
0 1 0 0 
0 0 0 3 
0 0 4 0 
_______
2 0 0 0 
0 1 0 0 
0 0 0 4 
0 0 3 0 
_______
2 0 0 0 
0 1 0 0 
0 0 4 0 
0 0 0 3 
_______
0 0 2 0 
0 1 0 0 
3 0 0 0 
0 0 0 4 
_______
0 0 2 0 
0 1 0 0 
0 0 0 3 
4 0 0 0 
_______
0 0 2 0 
0 1 0 0 
0 0 0 4 
3 0 0 0 
_______
0 0 2 0 
0 1 0 0 
4 0 0 0 
0 0 0 3 
_______
0 0 0 2 
0 1 0 0 
3 0 0 0 
0 0 4 0 
_______
0 0 0 2 
0 1 0 0 
0 0 3 0 
4 0 0 0 
_______
0 0 0 2 
0 1 0 0 
0 0 4 0 
3 0 0 0 
_______
0 0 0 2 
0 1 0 0 
4 0 0 0 
0 0 3 0 
_______
0 0 3 0 
0 1 0 0 
2 0 0 0 
0 0 0 4 
_______
0 0 0 3 
0 1 0 0 
2 0 0 0 
0 0 4 0 
_______
0 0 0 4 
0 1 0 0 
2 0 0 0 
0 0 3 0 
_______
0 0 4 0 
0 1 0 0 
2 0 0 0 
0 0 0 3 
_______
3 0 0 0 
0 1 0 0 
0 0 2 0 
0 0 0 4 
_______
0 0 0 3 
0 1 0 0 
0 0 2 0 
4 0 0 0 
_______
0 0 0 4 
0 1 0 0 
0 0 2 0 
3 0 0 0 
_______
4 0 0 0 
0 1 0 0 
0 0 2 0 
0 0 0 3 
_______
3 0 0 0 
0 1 0 0 
0 0 0 2 
0 0 4 0 
_______
0 0 3 0 
0 1 0 0 
0 0 0 2 
4 0 0 0 
_______
0 0 4 0 
0 1 0 0 
0 0 0 2 
3 0 0 0 
_______
4 0 0 0 
0 1 0 0 
0 0 0 2 
0 0 3 0 
_______
0 0 3 0 
0 1 0 0 
0 0 0 4 
2 0 0 0 
_______
0 0 0 3 
0 1 0 0 
0 0 4 0 
2 0 0 0 
_______
0 0 0 4 
0 1 0 0 
0 0 3 0 
2 0 0 0 
_______
0 0 4 0 
0 1 0 0 
0 0 0 3 
2 0 0 0 
_______
3 0 0 0 
0 1 0 0 
0 0 0 4 
0 0 2 0 
_______
0 0 0 3 
0 1 0 0 
4 0 0 0 
0 0 2 0 
_______
0 0 0 4 
0 1 0 0 
3 0 0 0 
0 0 2 0 
_______
4 0 0 0 
0 1 0 0 
0 0 0 3 
0 0 2 0 
_______
3 0 0 0 
0 1 0 0 
0 0 4 0 
0 0 0 2 
_______
0 0 3 0 
0 1 0 0 
4 0 0 0 
0 0 0 2 
_______
0 0 4 0 
0 1 0 0 
3 0 0 0 
0 0 0 2 
_______
4 0 0 0 
0 1 0 0 
0 0 3 0 
0 0 0 2 
_______
2 0 0 0 
0 0 1 0 
0 3 0 0 
0 0 0 4 
_______
2 0 0 0 
0 0 1 0 
0 0 0 3 
0 4 0 0 
_______
2 0 0 0 
0 0 1 0 
0 0 0 4 
0 3 0 0 
_______
2 0 0 0 
0 0 1 0 
0 4 0 0 
0 0 0 3 
_______
0 2 0 0 
0 0 1 0 
3 0 0 0 
0 0 0 4 
_______
0 2 0 0 
0 0 1 0 
0 0 0 3 
4 0 0 0 
_______
0 2 0 0 
0 0 1 0 
0 0 0 4 
3 0 0 0 
_______
0 2 0 0 
0 0 1 0 
4 0 0 0 
0 0 0 3 
_______
0 0 0 2 
0 0 1 0 
3 0 0 0 
0 4 0 0 
_______
0 0 0 2 
0 0 1 0 
0 3 0 0 
4 0 0 0 
_______
0 0 0 2 
0 0 1 0 
0 4 0 0 
3 0 0 0 
_______
0 0 0 2 
0 0 1 0 
4 0 0 0 
0 3 0 0 
_______
0 3 0 0 
0 0 1 0 
2 0 0 0 
0 0 0 4 
_______
0 0 0 3 
0 0 1 0 
2 0 0 0 
0 4 0 0 
_______
0 0 0 4 
0 0 1 0 
2 0 0 0 
0 3 0 0 
_______
0 4 0 0 
0 0 1 0 
2 0 0 0 
0 0 0 3 
_______
3 0 0 0 
0 0 1 0 
0 2 0 0 
0 0 0 4 
_______
0 0 0 3 
0 0 1 0 
0 2 0 0 
4 0 0 0 
_______
0 0 0 4 
0 0 1 0 
0 2 0 0 
3 0 0 0 
_______
4 0 0 0 
0 0 1 0 
0 2 0 0 
0 0 0 3 
_______
3 0 0 0 
0 0 1 0 
0 0 0 2 
0 4 0 0 
_______
0 3 0 0 
0 0 1 0 
0 0 0 2 
4 0 0 0 
_______
0 4 0 0 
0 0 1 0 
0 0 0 2 
3 0 0 0 
_______
4 0 0 0 
0 0 1 0 
0 0 0 2 
0 3 0 0 
_______
0 3 0 0 
0 0 1 0 
0 0 0 4 
2 0 0 0 
_______
0 0 0 3 
0 0 1 0 
0 4 0 0 
2 0 0 0 
_______
0 0 0 4 
0 0 1 0 
0 3 0 0 
2 0 0 0 
_______
0 4 0 0 
0 0 1 0 
0 0 0 3 
2 0 0 0 
_______
3 0 0 0 
0 0 1 0 
0 0 0 4 
0 2 0 0 
_______
0 0 0 3 
0 0 1 0 
4 0 0 0 
0 2 0 0 
_______
0 0 0 4 
0 0 1 0 
3 0 0 0 
0 2 0 0 
_______
4 0 0 0 
0 0 1 0 
0 0 0 3 
0 2 0 0 
_______
3 0 0 0 
0 0 1 0 
0 4 0 0 
0 0 0 2 
_______
0 3 0 0 
0 0 1 0 
4 0 0 0 
0 0 0 2 
_______
0 4 0 0 
0 0 1 0 
3 0 0 0 
0 0 0 2 
_______
4 0 0 0 
0 0 1 0 
0 3 0 0 
0 0 0 2 
_______
2 0 0 0 
0 0 0 1 
0 3 0 0 
0 0 4 0 
_______
2 0 0 0 
0 0 0 1 
0 0 3 0 
0 4 0 0 
_______
2 0 0 0 
0 0 0 1 
0 0 4 0 
0 3 0 0 
_______
2 0 0 0 
0 0 0 1 
0 4 0 0 
0 0 3 0 
_______
0 2 0 0 
0 0 0 1 
3 0 0 0 
0 0 4 0 
_______
0 2 0 0 
0 0 0 1 
0 0 3 0 
4 0 0 0 
_______
0 2 0 0 
0 0 0 1 
0 0 4 0 
3 0 0 0 
_______
0 2 0 0 
0 0 0 1 
4 0 0 0 
0 0 3 0 
_______
0 0 2 0 
0 0 0 1 
3 0 0 0 
0 4 0 0 
_______
0 0 2 0 
0 0 0 1 
0 3 0 0 
4 0 0 0 
_______
0 0 2 0 
0 0 0 1 
0 4 0 0 
3 0 0 0 
_______
0 0 2 0 
0 0 0 1 
4 0 0 0 
0 3 0 0 
_______
0 3 0 0 
0 0 0 1 
2 0 0 0 
0 0 4 0 
_______
0 0 3 0 
0 0 0 1 
2 0 0 0 
0 4 0 0 
_______
0 0 4 0 
0 0 0 1 
2 0 0 0 
0 3 0 0 
_______
0 4 0 0 
0 0 0 1 
2 0 0 0 
0 0 3 0 
_______
3 0 0 0 
0 0 0 1 
0 2 0 0 
0 0 4 0 
_______
0 0 3 0 
0 0 0 1 
0 2 0 0 
4 0 0 0 
_______
0 0 4 0 
0 0 0 1 
0 2 0 0 
3 0 0 0 
_______
4 0 0 0 
0 0 0 1 
0 2 0 0 
0 0 3 0 
_______
3 0 0 0 
0 0 0 1 
0 0 2 0 
0 4 0 0 
_______
0 3 0 0 
0 0 0 1 
0 0 2 0 
4 0 0 0 
_______
0 4 0 0 
0 0 0 1 
0 0 2 0 
3 0 0 0 
_______
4 0 0 0 
0 0 0 1 
0 0 2 0 
0 3 0 0 
_______
0 3 0 0 
0 0 0 1 
0 0 4 0 
2 0 0 0 
_______
0 0 3 0 
0 0 0 1 
0 4 0 0 
2 0 0 0 
_______
0 0 4 0 
0 0 0 1 
0 3 0 0 
2 0 0 0 
_______
0 4 0 0 
0 0 0 1 
0 0 3 0 
2 0 0 0 
_______
3 0 0 0 
0 0 0 1 
0 0 4 0 
0 2 0 0 
_______
0 0 3 0 
0 0 0 1 
4 0 0 0 
0 2 0 0 
_______
0 0 4 0 
0 0 0 1 
3 0 0 0 
0 2 0 0 
_______
4 0 0 0 
0 0 0 1 
0 0 3 0 
0 2 0 0 
_______
3 0 0 0 
0 0 0 1 
0 4 0 0 
0 0 2 0 
_______
0 3 0 0 
0 0 0 1 
4 0 0 0 
0 0 2 0 
_______
0 4 0 0 
0 0 0 1 
3 0 0 0 
0 0 2 0 
_______
4 0 0 0 
0 0 0 1 
0 3 0 0 
0 0 2 0 
_______
0 2 0 0 
0 0 3 0 
1 0 0 0 
0 0 0 4 
_______
0 2 0 0 
0 0 0 3 
1 0 0 0 
0 0 4 0 
_______
0 2 0 0 
0 0 0 4 
1 0 0 0 
0 0 3 0 
_______
0 2 0 0 
0 0 4 0 
1 0 0 0 
0 0 0 3 
_______
0 0 2 0 
0 3 0 0 
1 0 0 0 
0 0 0 4 
_______
0 0 2 0 
0 0 0 3 
1 0 0 0 
0 4 0 0 
_______
0 0 2 0 
0 0 0 4 
1 0 0 0 
0 3 0 0 
_______
0 0 2 0 
0 4 0 0 
1 0 0 0 
0 0 0 3 
_______
0 0 0 2 
0 3 0 0 
1 0 0 0 
0 0 4 0 
_______
0 0 0 2 
0 0 3 0 
1 0 0 0 
0 4 0 0 
_______
0 0 0 2 
0 0 4 0 
1 0 0 0 
0 3 0 0 
_______
0 0 0 2 
0 4 0 0 
1 0 0 0 
0 0 3 0 
_______
0 0 3 0 
0 2 0 0 
1 0 0 0 
0 0 0 4 
_______
0 0 0 3 
0 2 0 0 
1 0 0 0 
0 0 4 0 
_______
0 0 0 4 
0 2 0 0 
1 0 0 0 
0 0 3 0 
_______
0 0 4 0 
0 2 0 0 
1 0 0 0 
0 0 0 3 
_______
0 3 0 0 
0 0 2 0 
1 0 0 0 
0 0 0 4 
_______
0 0 0 3 
0 0 2 0 
1 0 0 0 
0 4 0 0 
_______
0 0 0 4 
0 0 2 0 
1 0 0 0 
0 3 0 0 
_______
0 4 0 0 
0 0 2 0 
1 0 0 0 
0 0 0 3 
_______
0 3 0 0 
0 0 0 2 
1 0 0 0 
0 0 4 0 
_______
0 0 3 0 
0 0 0 2 
1 0 0 0 
0 4 0 0 
_______
0 0 4 0 
0 0 0 2 
1 0 0 0 
0 3 0 0 
_______
0 4 0 0 
0 0 0 2 
1 0 0 0 
0 0 3 0 
_______
0 0 3 0 
0 0 0 4 
1 0 0 0 
0 2 0 0 
_______
0 0 0 3 
0 0 4 0 
1 0 0 0 
0 2 0 0 
_______
0 0 0 4 
0 0 3 0 
1 0 0 0 
0 2 0 0 
_______
0 0 4 0 
0 0 0 3 
1 0 0 0 
0 2 0 0 
_______
0 3 0 0 
0 0 0 4 
1 0 0 0 
0 0 2 0 
_______
0 0 0 3 
0 4 0 0 
1 0 0 0 
0 0 2 0 
_______
0 0 0 4 
0 3 0 0 
1 0 0 0 
0 0 2 0 
_______
0 4 0 0 
0 0 0 3 
1 0 0 0 
0 0 2 0 
_______
0 3 0 0 
0 0 4 0 
1 0 0 0 
0 0 0 2 
_______
0 0 3 0 
0 4 0 0 
1 0 0 0 
0 0 0 2 
_______
0 0 4 0 
0 3 0 0 
1 0 0 0 
0 0 0 2 
_______
0 4 0 0 
0 0 3 0 
1 0 0 0 
0 0 0 2 
_______
2 0 0 0 
0 0 3 0 
0 1 0 0 
0 0 0 4 
_______
2 0 0 0 
0 0 0 3 
0 1 0 0 
0 0 4 0 
_______
2 0 0 0 
0 0 0 4 
0 1 0 0 
0 0 3 0 
_______
2 0 0 0 
0 0 4 0 
0 1 0 0 
0 0 0 3 
_______
0 0 2 0 
3 0 0 0 
0 1 0 0 
0 0 0 4 
_______
0 0 2 0 
0 0 0 3 
0 1 0 0 
4 0 0 0 
_______
0 0 2 0 
0 0 0 4 
0 1 0 0 
3 0 0 0 
_______
0 0 2 0 
4 0 0 0 
0 1 0 0 
0 0 0 3 
_______
0 0 0 2 
3 0 0 0 
0 1 0 0 
0 0 4 0 
_______
0 0 0 2 
0 0 3 0 
0 1 0 0 
4 0 0 0 
_______
0 0 0 2 
0 0 4 0 
0 1 0 0 
3 0 0 0 
_______
0 0 0 2 
4 0 0 0 
0 1 0 0 
0 0 3 0 
_______
0 0 3 0 
2 0 0 0 
0 1 0 0 
0 0 0 4 
_______
0 0 0 3 
2 0 0 0 
0 1 0 0 
0 0 4 0 
_______
0 0 0 4 
2 0 0 0 
0 1 0 0 
0 0 3 0 
_______
0 0 4 0 
2 0 0 0 
0 1 0 0 
0 0 0 3 
_______
3 0 0 0 
0 0 2 0 
0 1 0 0 
0 0 0 4 
_______
0 0 0 3 
0 0 2 0 
0 1 0 0 
4 0 0 0 
_______
0 0 0 4 
0 0 2 0 
0 1 0 0 
3 0 0 0 
_______
4 0 0 0 
0 0 2 0 
0 1 0 0 
0 0 0 3 
_______
3 0 0 0 
0 0 0 2 
0 1 0 0 
0 0 4 0 
_______
0 0 3 0 
0 0 0 2 
0 1 0 0 
4 0 0 0 
_______
0 0 4 0 
0 0 0 2 
0 1 0 0 
3 0 0 0 
_______
4 0 0 0 
0 0 0 2 
0 1 0 0 
0 0 3 0 
_______
0 0 3 0 
0 0 0 4 
0 1 0 0 
2 0 0 0 
_______
0 0 0 3 
0 0 4 0 
0 1 0 0 
2 0 0 0 
_______
0 0 0 4 
0 0 3 0 
0 1 0 0 
2 0 0 0 
_______
0 0 4 0 
0 0 0 3 
0 1 0 0 
2 0 0 0 
_______
3 0 0 0 
0 0 0 4 
0 1 0 0 
0 0 2 0 
_______
0 0 0 3 
4 0 0 0 
0 1 0 0 
0 0 2 0 
_______
0 0 0 4 
3 0 0 0 
0 1 0 0 
0 0 2 0 
_______
4 0 0 0 
0 0 0 3 
0 1 0 0 
0 0 2 0 
_______
3 0 0 0 
0 0 4 0 
0 1 0 0 
0 0 0 2 
_______
0 0 3 0 
4 0 0 0 
0 1 0 0 
0 0 0 2 
_______
0 0 4 0 
3 0 0 0 
0 1 0 0 
0 0 0 2 
_______
4 0 0 0 
0 0 3 0 
0 1 0 0 
0 0 0 2 
_______
2 0 0 0 
0 3 0 0 
0 0 1 0 
0 0 0 4 
_______
2 0 0 0 
0 0 0 3 
0 0 1 0 
0 4 0 0 
_______
2 0 0 0 
0 0 0 4 
0 0 1 0 
0 3 0 0 
_______
2 0 0 0 
0 4 0 0 
0 0 1 0 
0 0 0 3 
_______
0 2 0 0 
3 0 0 0 
0 0 1 0 
0 0 0 4 
_______
0 2 0 0 
0 0 0 3 
0 0 1 0 
4 0 0 0 
_______
0 2 0 0 
0 0 0 4 
0 0 1 0 
3 0 0 0 
_______
0 2 0 0 
4 0 0 0 
0 0 1 0 
0 0 0 3 
_______
0 0 0 2 
3 0 0 0 
0 0 1 0 
0 4 0 0 
_______
0 0 0 2 
0 3 0 0 
0 0 1 0 
4 0 0 0 
_______
0 0 0 2 
0 4 0 0 
0 0 1 0 
3 0 0 0 
_______
0 0 0 2 
4 0 0 0 
0 0 1 0 
0 3 0 0 
_______
0 3 0 0 
2 0 0 0 
0 0 1 0 
0 0 0 4 
_______
0 0 0 3 
2 0 0 0 
0 0 1 0 
0 4 0 0 
_______
0 0 0 4 
2 0 0 0 
0 0 1 0 
0 3 0 0 
_______
0 4 0 0 
2 0 0 0 
0 0 1 0 
0 0 0 3 
_______
3 0 0 0 
0 2 0 0 
0 0 1 0 
0 0 0 4 
_______
0 0 0 3 
0 2 0 0 
0 0 1 0 
4 0 0 0 
_______
0 0 0 4 
0 2 0 0 
0 0 1 0 
3 0 0 0 
_______
4 0 0 0 
0 2 0 0 
0 0 1 0 
0 0 0 3 
_______
3 0 0 0 
0 0 0 2 
0 0 1 0 
0 4 0 0 
_______
0 3 0 0 
0 0 0 2 
0 0 1 0 
4 0 0 0 
_______
0 4 0 0 
0 0 0 2 
0 0 1 0 
3 0 0 0 
_______
4 0 0 0 
0 0 0 2 
0 0 1 0 
0 3 0 0 
_______
0 3 0 0 
0 0 0 4 
0 0 1 0 
2 0 0 0 
_______
0 0 0 3 
0 4 0 0 
0 0 1 0 
2 0 0 0 
_______
0 0 0 4 
0 3 0 0 
0 0 1 0 
2 0 0 0 
_______
0 4 0 0 
0 0 0 3 
0 0 1 0 
2 0 0 0 
_______
3 0 0 0 
0 0 0 4 
0 0 1 0 
0 2 0 0 
_______
0 0 0 3 
4 0 0 0 
0 0 1 0 
0 2 0 0 
_______
0 0 0 4 
3 0 0 0 
0 0 1 0 
0 2 0 0 
_______
4 0 0 0 
0 0 0 3 
0 0 1 0 
0 2 0 0 
_______
3 0 0 0 
0 4 0 0 
0 0 1 0 
0 0 0 2 
_______
0 3 0 0 
4 0 0 0 
0 0 1 0 
0 0 0 2 
_______
0 4 0 0 
3 0 0 0 
0 0 1 0 
0 0 0 2 
_______
4 0 0 0 
0 3 0 0 
0 0 1 0 
0 0 0 2 
_______
2 0 0 0 
0 3 0 0 
0 0 0 1 
0 0 4 0 
_______
2 0 0 0 
0 0 3 0 
0 0 0 1 
0 4 0 0 
_______
2 0 0 0 
0 0 4 0 
0 0 0 1 
0 3 0 0 
_______
2 0 0 0 
0 4 0 0 
0 0 0 1 
0 0 3 0 
_______
0 2 0 0 
3 0 0 0 
0 0 0 1 
0 0 4 0 
_______
0 2 0 0 
0 0 3 0 
0 0 0 1 
4 0 0 0 
_______
0 2 0 0 
0 0 4 0 
0 0 0 1 
3 0 0 0 
_______
0 2 0 0 
4 0 0 0 
0 0 0 1 
0 0 3 0 
_______
0 0 2 0 
3 0 0 0 
0 0 0 1 
0 4 0 0 
_______
0 0 2 0 
0 3 0 0 
0 0 0 1 
4 0 0 0 
_______
0 0 2 0 
0 4 0 0 
0 0 0 1 
3 0 0 0 
_______
0 0 2 0 
4 0 0 0 
0 0 0 1 
0 3 0 0 
_______
0 3 0 0 
2 0 0 0 
0 0 0 1 
0 0 4 0 
_______
0 0 3 0 
2 0 0 0 
0 0 0 1 
0 4 0 0 
_______
0 0 4 0 
2 0 0 0 
0 0 0 1 
0 3 0 0 
_______
0 4 0 0 
2 0 0 0 
0 0 0 1 
0 0 3 0 
_______
3 0 0 0 
0 2 0 0 
0 0 0 1 
0 0 4 0 
_______
0 0 3 0 
0 2 0 0 
0 0 0 1 
4 0 0 0 
_______
0 0 4 0 
0 2 0 0 
0 0 0 1 
3 0 0 0 
_______
4 0 0 0 
0 2 0 0 
0 0 0 1 
0 0 3 0 
_______
3 0 0 0 
0 0 2 0 
0 0 0 1 
0 4 0 0 
_______
0 3 0 0 
0 0 2 0 
0 0 0 1 
4 0 0 0 
_______
0 4 0 0 
0 0 2 0 
0 0 0 1 
3 0 0 0 
_______
4 0 0 0 
0 0 2 0 
0 0 0 1 
0 3 0 0 
_______
0 3 0 0 
0 0 4 0 
0 0 0 1 
2 0 0 0 
_______
0 0 3 0 
0 4 0 0 
0 0 0 1 
2 0 0 0 
_______
0 0 4 0 
0 3 0 0 
0 0 0 1 
2 0 0 0 
_______
0 4 0 0 
0 0 3 0 
0 0 0 1 
2 0 0 0 
_______
3 0 0 0 
0 0 4 0 
0 0 0 1 
0 2 0 0 
_______
0 0 3 0 
4 0 0 0 
0 0 0 1 
0 2 0 0 
_______
0 0 4 0 
3 0 0 0 
0 0 0 1 
0 2 0 0 
_______
4 0 0 0 
0 0 3 0 
0 0 0 1 
0 2 0 0 
_______
3 0 0 0 
0 4 0 0 
0 0 0 1 
0 0 2 0 
_______
0 3 0 0 
4 0 0 0 
0 0 0 1 
0 0 2 0 
_______
0 4 0 0 
3 0 0 0 
0 0 0 1 
0 0 2 0 
_______
4 0 0 0 
0 3 0 0 
0 0 0 1 
0 0 2 0 
_______
0 2 0 0 
0 0 3 0 
0 0 0 4 
1 0 0 0 
_______
0 2 0 0 
0 0 0 3 
0 0 4 0 
1 0 0 0 
_______
0 2 0 0 
0 0 0 4 
0 0 3 0 
1 0 0 0 
_______
0 2 0 0 
0 0 4 0 
0 0 0 3 
1 0 0 0 
_______
0 0 2 0 
0 3 0 0 
0 0 0 4 
1 0 0 0 
_______
0 0 2 0 
0 0 0 3 
0 4 0 0 
1 0 0 0 
_______
0 0 2 0 
0 0 0 4 
0 3 0 0 
1 0 0 0 
_______
0 0 2 0 
0 4 0 0 
0 0 0 3 
1 0 0 0 
_______
0 0 0 2 
0 3 0 0 
0 0 4 0 
1 0 0 0 
_______
0 0 0 2 
0 0 3 0 
0 4 0 0 
1 0 0 0 
_______
0 0 0 2 
0 0 4 0 
0 3 0 0 
1 0 0 0 
_______
0 0 0 2 
0 4 0 0 
0 0 3 0 
1 0 0 0 
_______
0 0 3 0 
0 2 0 0 
0 0 0 4 
1 0 0 0 
_______
0 0 0 3 
0 2 0 0 
0 0 4 0 
1 0 0 0 
_______
0 0 0 4 
0 2 0 0 
0 0 3 0 
1 0 0 0 
_______
0 0 4 0 
0 2 0 0 
0 0 0 3 
1 0 0 0 
_______
0 3 0 0 
0 0 2 0 
0 0 0 4 
1 0 0 0 
_______
0 0 0 3 
0 0 2 0 
0 4 0 0 
1 0 0 0 
_______
0 0 0 4 
0 0 2 0 
0 3 0 0 
1 0 0 0 
_______
0 4 0 0 
0 0 2 0 
0 0 0 3 
1 0 0 0 
_______
0 3 0 0 
0 0 0 2 
0 0 4 0 
1 0 0 0 
_______
0 0 3 0 
0 0 0 2 
0 4 0 0 
1 0 0 0 
_______
0 0 4 0 
0 0 0 2 
0 3 0 0 
1 0 0 0 
_______
0 4 0 0 
0 0 0 2 
0 0 3 0 
1 0 0 0 
_______
0 0 3 0 
0 0 0 4 
0 2 0 0 
1 0 0 0 
_______
0 0 0 3 
0 0 4 0 
0 2 0 0 
1 0 0 0 
_______
0 0 0 4 
0 0 3 0 
0 2 0 0 
1 0 0 0 
_______
0 0 4 0 
0 0 0 3 
0 2 0 0 
1 0 0 0 
_______
0 3 0 0 
0 0 0 4 
0 0 2 0 
1 0 0 0 
_______
0 0 0 3 
0 4 0 0 
0 0 2 0 
1 0 0 0 
_______
0 0 0 4 
0 3 0 0 
0 0 2 0 
1 0 0 0 
_______
0 4 0 0 
0 0 0 3 
0 0 2 0 
1 0 0 0 
_______
0 3 0 0 
0 0 4 0 
0 0 0 2 
1 0 0 0 
_______
0 0 3 0 
0 4 0 0 
0 0 0 2 
1 0 0 0 
_______
0 0 4 0 
0 3 0 0 
0 0 0 2 
1 0 0 0 
_______
0 4 0 0 
0 0 3 0 
0 0 0 2 
1 0 0 0 
_______
2 0 0 0 
0 0 3 0 
0 0 0 4 
0 1 0 0 
_______
2 0 0 0 
0 0 0 3 
0 0 4 0 
0 1 0 0 
_______
2 0 0 0 
0 0 0 4 
0 0 3 0 
0 1 0 0 
_______
2 0 0 0 
0 0 4 0 
0 0 0 3 
0 1 0 0 
_______
0 0 2 0 
3 0 0 0 
0 0 0 4 
0 1 0 0 
_______
0 0 2 0 
0 0 0 3 
4 0 0 0 
0 1 0 0 
_______
0 0 2 0 
0 0 0 4 
3 0 0 0 
0 1 0 0 
_______
0 0 2 0 
4 0 0 0 
0 0 0 3 
0 1 0 0 
_______
0 0 0 2 
3 0 0 0 
0 0 4 0 
0 1 0 0 
_______
0 0 0 2 
0 0 3 0 
4 0 0 0 
0 1 0 0 
_______
0 0 0 2 
0 0 4 0 
3 0 0 0 
0 1 0 0 
_______
0 0 0 2 
4 0 0 0 
0 0 3 0 
0 1 0 0 
_______
0 0 3 0 
2 0 0 0 
0 0 0 4 
0 1 0 0 
_______
0 0 0 3 
2 0 0 0 
0 0 4 0 
0 1 0 0 
_______
0 0 0 4 
2 0 0 0 
0 0 3 0 
0 1 0 0 
_______
0 0 4 0 
2 0 0 0 
0 0 0 3 
0 1 0 0 
_______
3 0 0 0 
0 0 2 0 
0 0 0 4 
0 1 0 0 
_______
0 0 0 3 
0 0 2 0 
4 0 0 0 
0 1 0 0 
_______
0 0 0 4 
0 0 2 0 
3 0 0 0 
0 1 0 0 
_______
4 0 0 0 
0 0 2 0 
0 0 0 3 
0 1 0 0 
_______
3 0 0 0 
0 0 0 2 
0 0 4 0 
0 1 0 0 
_______
0 0 3 0 
0 0 0 2 
4 0 0 0 
0 1 0 0 
_______
0 0 4 0 
0 0 0 2 
3 0 0 0 
0 1 0 0 
_______
4 0 0 0 
0 0 0 2 
0 0 3 0 
0 1 0 0 
_______
0 0 3 0 
0 0 0 4 
2 0 0 0 
0 1 0 0 
_______
0 0 0 3 
0 0 4 0 
2 0 0 0 
0 1 0 0 
_______
0 0 0 4 
0 0 3 0 
2 0 0 0 
0 1 0 0 
_______
0 0 4 0 
0 0 0 3 
2 0 0 0 
0 1 0 0 
_______
3 0 0 0 
0 0 0 4 
0 0 2 0 
0 1 0 0 
_______
0 0 0 3 
4 0 0 0 
0 0 2 0 
0 1 0 0 
_______
0 0 0 4 
3 0 0 0 
0 0 2 0 
0 1 0 0 
_______
4 0 0 0 
0 0 0 3 
0 0 2 0 
0 1 0 0 
_______
3 0 0 0 
0 0 4 0 
0 0 0 2 
0 1 0 0 
_______
0 0 3 0 
4 0 0 0 
0 0 0 2 
0 1 0 0 
_______
0 0 4 0 
3 0 0 0 
0 0 0 2 
0 1 0 0 
_______
4 0 0 0 
0 0 3 0 
0 0 0 2 
0 1 0 0 
_______
2 0 0 0 
0 3 0 0 
0 0 0 4 
0 0 1 0 
_______
2 0 0 0 
0 0 0 3 
0 4 0 0 
0 0 1 0 
_______
2 0 0 0 
0 0 0 4 
0 3 0 0 
0 0 1 0 
_______
2 0 0 0 
0 4 0 0 
0 0 0 3 
0 0 1 0 
_______
0 2 0 0 
3 0 0 0 
0 0 0 4 
0 0 1 0 
_______
0 2 0 0 
0 0 0 3 
4 0 0 0 
0 0 1 0 
_______
0 2 0 0 
0 0 0 4 
3 0 0 0 
0 0 1 0 
_______
0 2 0 0 
4 0 0 0 
0 0 0 3 
0 0 1 0 
_______
0 0 0 2 
3 0 0 0 
0 4 0 0 
0 0 1 0 
_______
0 0 0 2 
0 3 0 0 
4 0 0 0 
0 0 1 0 
_______
0 0 0 2 
0 4 0 0 
3 0 0 0 
0 0 1 0 
_______
0 0 0 2 
4 0 0 0 
0 3 0 0 
0 0 1 0 
_______
0 3 0 0 
2 0 0 0 
0 0 0 4 
0 0 1 0 
_______
0 0 0 3 
2 0 0 0 
0 4 0 0 
0 0 1 0 
_______
0 0 0 4 
2 0 0 0 
0 3 0 0 
0 0 1 0 
_______
0 4 0 0 
2 0 0 0 
0 0 0 3 
0 0 1 0 
_______
3 0 0 0 
0 2 0 0 
0 0 0 4 
0 0 1 0 
_______
0 0 0 3 
0 2 0 0 
4 0 0 0 
0 0 1 0 
_______
0 0 0 4 
0 2 0 0 
3 0 0 0 
0 0 1 0 
_______
4 0 0 0 
0 2 0 0 
0 0 0 3 
0 0 1 0 
_______
3 0 0 0 
0 0 0 2 
0 4 0 0 
0 0 1 0 
_______
0 3 0 0 
0 0 0 2 
4 0 0 0 
0 0 1 0 
_______
0 4 0 0 
0 0 0 2 
3 0 0 0 
0 0 1 0 
_______
4 0 0 0 
0 0 0 2 
0 3 0 0 
0 0 1 0 
_______
0 3 0 0 
0 0 0 4 
2 0 0 0 
0 0 1 0 
_______
0 0 0 3 
0 4 0 0 
2 0 0 0 
0 0 1 0 
_______
0 0 0 4 
0 3 0 0 
2 0 0 0 
0 0 1 0 
_______
0 4 0 0 
0 0 0 3 
2 0 0 0 
0 0 1 0 
_______
3 0 0 0 
0 0 0 4 
0 2 0 0 
0 0 1 0 
_______
0 0 0 3 
4 0 0 0 
0 2 0 0 
0 0 1 0 
_______
0 0 0 4 
3 0 0 0 
0 2 0 0 
0 0 1 0 
_______
4 0 0 0 
0 0 0 3 
0 2 0 0 
0 0 1 0 
_______
3 0 0 0 
0 4 0 0 
0 0 0 2 
0 0 1 0 
_______
0 3 0 0 
4 0 0 0 
0 0 0 2 
0 0 1 0 
_______
0 4 0 0 
3 0 0 0 
0 0 0 2 
0 0 1 0 
_______
4 0 0 0 
0 3 0 0 
0 0 0 2 
0 0 1 0 
_______
2 0 0 0 
0 3 0 0 
0 0 4 0 
0 0 0 1 
_______
2 0 0 0 
0 0 3 0 
0 4 0 0 
0 0 0 1 
_______
2 0 0 0 
0 0 4 0 
0 3 0 0 
0 0 0 1 
_______
2 0 0 0 
0 4 0 0 
0 0 3 0 
0 0 0 1 
_______
0 2 0 0 
3 0 0 0 
0 0 4 0 
0 0 0 1 
_______
0 2 0 0 
0 0 3 0 
4 0 0 0 
0 0 0 1 
_______
0 2 0 0 
0 0 4 0 
3 0 0 0 
0 0 0 1 
_______
0 2 0 0 
4 0 0 0 
0 0 3 0 
0 0 0 1 
_______
0 0 2 0 
3 0 0 0 
0 4 0 0 
0 0 0 1 
_______
0 0 2 0 
0 3 0 0 
4 0 0 0 
0 0 0 1 
_______
0 0 2 0 
0 4 0 0 
3 0 0 0 
0 0 0 1 
_______
0 0 2 0 
4 0 0 0 
0 3 0 0 
0 0 0 1 
_______
0 3 0 0 
2 0 0 0 
0 0 4 0 
0 0 0 1 
_______
0 0 3 0 
2 0 0 0 
0 4 0 0 
0 0 0 1 
_______
0 0 4 0 
2 0 0 0 
0 3 0 0 
0 0 0 1 
_______
0 4 0 0 
2 0 0 0 
0 0 3 0 
0 0 0 1 
_______
3 0 0 0 
0 2 0 0 
0 0 4 0 
0 0 0 1 
_______
0 0 3 0 
0 2 0 0 
4 0 0 0 
0 0 0 1 
_______
0 0 4 0 
0 2 0 0 
3 0 0 0 
0 0 0 1 
_______
4 0 0 0 
0 2 0 0 
0 0 3 0 
0 0 0 1 
_______
3 0 0 0 
0 0 2 0 
0 4 0 0 
0 0 0 1 
_______
0 3 0 0 
0 0 2 0 
4 0 0 0 
0 0 0 1 
_______
0 4 0 0 
0 0 2 0 
3 0 0 0 
0 0 0 1 
_______
4 0 0 0 
0 0 2 0 
0 3 0 0 
0 0 0 1 
_______
0 3 0 0 
0 0 4 0 
2 0 0 0 
0 0 0 1 
_______
0 0 3 0 
0 4 0 0 
2 0 0 0 
0 0 0 1 
_______
0 0 4 0 
0 3 0 0 
2 0 0 0 
0 0 0 1 
_______
0 4 0 0 
0 0 3 0 
2 0 0 0 
0 0 0 1 
_______
3 0 0 0 
0 0 4 0 
0 2 0 0 
0 0 0 1 
_______
0 0 3 0 
4 0 0 0 
0 2 0 0 
0 0 0 1 
_______
0 0 4 0 
3 0 0 0 
0 2 0 0 
0 0 0 1 
_______
4 0 0 0 
0 0 3 0 
0 2 0 0 
0 0 0 1 
_______
3 0 0 0 
0 4 0 0 
0 0 2 0 
0 0 0 1 
_______
0 3 0 0 
4 0 0 0 
0 0 2 0 
0 0 0 1 
_______
0 4 0 0 
3 0 0 0 
0 0 2 0 
0 0 0 1 
_______
4 0 0 0 
0 3 0 0 
0 0 2 0 
0 0 0 1 
_______
Number of answers : 576
___________________________________
behrad@TadavomnisT:~/Desktop$

مساله nوزیر - برای n = 4 (بی‌تفاوت):
تابع رو بصورت زیر فراخونی کنید:

n_queens( 4 );

و خروجی این قسمت :

behrad@TadavomnisT:~/Desktop$ php back_tracking.php 

** 4 QUEENS ** (no distinguish between queens)
Building empty matrix...
Building decision tree...
Printing decision tree :
.
└── "root"
    ├── [0,0]
    │   ├── [1,2]
    │   │   └── [3,1]
    │   ├── [1,3]
    │   │   ├── [2,1]
    │   │   └── [3,2]
    │   ├── [2,1]
    │   │   └── [1,3]
    │   ├── [2,3]
    │   │   └── [3,1]
    │   ├── [3,1]
    │   │   ├── [1,2]
    │   │   └── [2,3]
    │   └── [3,2]
    │       └── [1,3]
    ├── [0,1]
    │   ├── [1,3]
    │   │   ├── [2,0]
    │   │   │   └── [3,2]
    │   │   ├── [3,0]
    │   │   └── [3,2]
    │   │       └── [2,0]
    │   ├── [2,0]
    │   │   ├── [1,3]
    │   │   │   └── [3,2]
    │   │   ├── [3,2]
    │   │   │   └── [1,3]
    │   │   └── [3,3]
    │   ├── [2,2]
    │   │   └── [3,0]
    │   ├── [3,0]
    │   │   ├── [1,3]
    │   │   └── [2,2]
    │   ├── [3,2]
    │   │   ├── [1,3]
    │   │   │   └── [2,0]
    │   │   └── [2,0]
    │   │       └── [1,3]
    │   └── [3,3]
    │       └── [2,0]
    ├── [0,2]
    │   ├── [1,0]
    │   │   ├── [2,3]
    │   │   │   └── [3,1]
    │   │   ├── [3,1]
    │   │   │   └── [2,3]
    │   │   └── [3,3]
    │   ├── [2,1]
    │   │   └── [3,3]
    │   ├── [2,3]
    │   │   ├── [1,0]
    │   │   │   └── [3,1]
    │   │   ├── [3,0]
    │   │   └── [3,1]
    │   │       └── [1,0]
    │   ├── [3,0]
    │   │   └── [2,3]
    │   ├── [3,1]
    │   │   ├── [1,0]
    │   │   │   └── [2,3]
    │   │   └── [2,3]
    │   │       └── [1,0]
    │   └── [3,3]
    │       ├── [1,0]
    │       └── [2,1]
    ├── [0,3]
    │   ├── [1,0]
    │   │   ├── [2,2]
    │   │   └── [3,1]
    │   ├── [1,1]
    │   │   └── [3,2]
    │   ├── [2,0]
    │   │   └── [3,2]
    │   ├── [2,2]
    │   │   └── [1,0]
    │   ├── [3,1]
    │   │   └── [1,0]
    │   └── [3,2]
    │       ├── [1,1]
    │       └── [2,0]
    ├── [1,0]
    │   ├── [0,2]
    │   │   ├── [2,3]
    │   │   │   └── [3,1]
    │   │   ├── [3,1]
    │   │   │   └── [2,3]
    │   │   └── [3,3]
    │   ├── [0,3]
    │   │   ├── [2,2]
    │   │   └── [3,1]
    │   ├── [2,2]
    │   │   └── [0,3]
    │   ├── [2,3]
    │   │   ├── [0,2]
    │   │   │   └── [3,1]
    │   │   └── [3,1]
    │   │       └── [0,2]
    │   ├── [3,1]
    │   │   ├── [0,2]
    │   │   │   └── [2,3]
    │   │   ├── [0,3]
    │   │   └── [2,3]
    │   │       └── [0,2]
    │   └── [3,3]
    │       └── [0,2]
    ├── [1,1]
    │   ├── [0,3]
    │   │   └── [3,2]
    │   ├── [2,3]
    │   │   └── [3,0]
    │   ├── [3,0]
    │   │   └── [2,3]
    │   └── [3,2]
    │       └── [0,3]
    ├── [1,2]
    │   ├── [0,0]
    │   │   └── [3,1]
    │   ├── [2,0]
    │   │   └── [3,3]
    │   ├── [3,1]
    │   │   └── [0,0]
    │   └── [3,3]
    │       └── [2,0]
    ├── [1,3]
    │   ├── [0,0]
    │   │   ├── [2,1]
    │   │   └── [3,2]
    │   ├── [0,1]
    │   │   ├── [2,0]
    │   │   │   └── [3,2]
    │   │   ├── [3,0]
    │   │   └── [3,2]
    │   │       └── [2,0]
    │   ├── [2,0]
    │   │   ├── [0,1]
    │   │   │   └── [3,2]
    │   │   └── [3,2]
    │   │       └── [0,1]
    │   ├── [2,1]
    │   │   └── [0,0]
    │   ├── [3,0]
    │   │   └── [0,1]
    │   └── [3,2]
    │       ├── [0,0]
    │       ├── [0,1]
    │       │   └── [2,0]
    │       └── [2,0]
    │           └── [0,1]
    ├── [2,0]
    │   ├── [0,1]
    │   │   ├── [1,3]
    │   │   │   └── [3,2]
    │   │   ├── [3,2]
    │   │   │   └── [1,3]
    │   │   └── [3,3]
    │   ├── [0,3]
    │   │   └── [3,2]
    │   ├── [1,2]
    │   │   └── [3,3]
    │   ├── [1,3]
    │   │   ├── [0,1]
    │   │   │   └── [3,2]
    │   │   └── [3,2]
    │   │       └── [0,1]
    │   ├── [3,2]
    │   │   ├── [0,1]
    │   │   │   └── [1,3]
    │   │   ├── [0,3]
    │   │   └── [1,3]
    │   │       └── [0,1]
    │   └── [3,3]
    │       ├── [0,1]
    │       └── [1,2]
    ├── [2,1]
    │   ├── [0,0]
    │   │   └── [1,3]
    │   ├── [0,2]
    │   │   └── [3,3]
    │   ├── [1,3]
    │   │   └── [0,0]
    │   └── [3,3]
    │       └── [0,2]
    ├── [2,2]
    │   ├── [0,1]
    │   │   └── [3,0]
    │   ├── [0,3]
    │   │   └── [1,0]
    │   ├── [1,0]
    │   │   └── [0,3]
    │   └── [3,0]
    │       └── [0,1]
    ├── [2,3]
    │   ├── [0,0]
    │   │   └── [3,1]
    │   ├── [0,2]
    │   │   ├── [1,0]
    │   │   │   └── [3,1]
    │   │   ├── [3,0]
    │   │   └── [3,1]
    │   │       └── [1,0]
    │   ├── [1,0]
    │   │   ├── [0,2]
    │   │   │   └── [3,1]
    │   │   └── [3,1]
    │   │       └── [0,2]
    │   ├── [1,1]
    │   │   └── [3,0]
    │   ├── [3,0]
    │   │   ├── [0,2]
    │   │   └── [1,1]
    │   └── [3,1]
    │       ├── [0,0]
    │       ├── [0,2]
    │       │   └── [1,0]
    │       └── [1,0]
    │           └── [0,2]
    ├── [3,0]
    │   ├── [0,1]
    │   │   ├── [1,3]
    │   │   └── [2,2]
    │   ├── [0,2]
    │   │   └── [2,3]
    │   ├── [1,1]
    │   │   └── [2,3]
    │   ├── [1,3]
    │   │   └── [0,1]
    │   ├── [2,2]
    │   │   └── [0,1]
    │   └── [2,3]
    │       ├── [0,2]
    │       └── [1,1]
    ├── [3,1]
    │   ├── [0,0]
    │   │   ├── [1,2]
    │   │   └── [2,3]
    │   ├── [0,2]
    │   │   ├── [1,0]
    │   │   │   └── [2,3]
    │   │   └── [2,3]
    │   │       └── [1,0]
    │   ├── [0,3]
    │   │   └── [1,0]
    │   ├── [1,0]
    │   │   ├── [0,2]
    │   │   │   └── [2,3]
    │   │   ├── [0,3]
    │   │   └── [2,3]
    │   │       └── [0,2]
    │   ├── [1,2]
    │   │   └── [0,0]
    │   └── [2,3]
    │       ├── [0,0]
    │       ├── [0,2]
    │       │   └── [1,0]
    │       └── [1,0]
    │           └── [0,2]
    ├── [3,2]
    │   ├── [0,0]
    │   │   └── [1,3]
    │   ├── [0,1]
    │   │   ├── [1,3]
    │   │   │   └── [2,0]
    │   │   └── [2,0]
    │   │       └── [1,3]
    │   ├── [0,3]
    │   │   ├── [1,1]
    │   │   └── [2,0]
    │   ├── [1,1]
    │   │   └── [0,3]
    │   ├── [1,3]
    │   │   ├── [0,0]
    │   │   ├── [0,1]
    │   │   │   └── [2,0]
    │   │   └── [2,0]
    │   │       └── [0,1]
    │   └── [2,0]
    │       ├── [0,1]
    │       │   └── [1,3]
    │       ├── [0,3]
    │       └── [1,3]
    │           └── [0,1]
    └── [3,3]
        ├── [0,1]
        │   └── [2,0]
        ├── [0,2]
        │   ├── [1,0]
        │   └── [2,1]
        ├── [1,0]
        │   └── [0,2]
        ├── [1,2]
        │   └── [2,0]
        ├── [2,0]
        │   ├── [0,1]
        │   └── [1,2]
        └── [2,1]
            └── [0,2]

Printing all possible solutions :
0 1 0 0 
0 0 0 1 
1 0 0 0 
0 0 1 0 
_______
0 0 1 0 
1 0 0 0 
0 0 0 1 
0 1 0 0 
_______
Number of answers : 2
Number of symmetric answers : 0
___________________________________
behrad@TadavomnisT:~/Desktop$

مساله nوزیر - برای n = 4 (باتفاوت):
تابع رو بصورت زیر فراخونی کنید:

n_queens( 4 , true ); //distinguish between queens

و خروجی این قسمت :

behrad@TadavomnisT:~/Desktop$ php back_tracking.php 

** 4 QUEENS ** (distinguishing between queens)
Building empty matrix...
Building decision tree...
Printing decision tree :
.
└── "root"
    ├── [0,0]
    │   ├── [1,2]
    │   │   └── [3,1]
    │   ├── [1,3]
    │   │   ├── [2,1]
    │   │   └── [3,2]
    │   ├── [2,1]
    │   │   └── [1,3]
    │   ├── [2,3]
    │   │   └── [3,1]
    │   ├── [3,1]
    │   │   ├── [1,2]
    │   │   └── [2,3]
    │   └── [3,2]
    │       └── [1,3]
    ├── [0,1]
    │   ├── [1,3]
    │   │   ├── [2,0]
    │   │   │   └── [3,2]
    │   │   ├── [3,0]
    │   │   └── [3,2]
    │   │       └── [2,0]
    │   ├── [2,0]
    │   │   ├── [1,3]
    │   │   │   └── [3,2]
    │   │   ├── [3,2]
    │   │   │   └── [1,3]
    │   │   └── [3,3]
    │   ├── [2,2]
    │   │   └── [3,0]
    │   ├── [3,0]
    │   │   ├── [1,3]
    │   │   └── [2,2]
    │   ├── [3,2]
    │   │   ├── [1,3]
    │   │   │   └── [2,0]
    │   │   └── [2,0]
    │   │       └── [1,3]
    │   └── [3,3]
    │       └── [2,0]
    ├── [0,2]
    │   ├── [1,0]
    │   │   ├── [2,3]
    │   │   │   └── [3,1]
    │   │   ├── [3,1]
    │   │   │   └── [2,3]
    │   │   └── [3,3]
    │   ├── [2,1]
    │   │   └── [3,3]
    │   ├── [2,3]
    │   │   ├── [1,0]
    │   │   │   └── [3,1]
    │   │   ├── [3,0]
    │   │   └── [3,1]
    │   │       └── [1,0]
    │   ├── [3,0]
    │   │   └── [2,3]
    │   ├── [3,1]
    │   │   ├── [1,0]
    │   │   │   └── [2,3]
    │   │   └── [2,3]
    │   │       └── [1,0]
    │   └── [3,3]
    │       ├── [1,0]
    │       └── [2,1]
    ├── [0,3]
    │   ├── [1,0]
    │   │   ├── [2,2]
    │   │   └── [3,1]
    │   ├── [1,1]
    │   │   └── [3,2]
    │   ├── [2,0]
    │   │   └── [3,2]
    │   ├── [2,2]
    │   │   └── [1,0]
    │   ├── [3,1]
    │   │   └── [1,0]
    │   └── [3,2]
    │       ├── [1,1]
    │       └── [2,0]
    ├── [1,0]
    │   ├── [0,2]
    │   │   ├── [2,3]
    │   │   │   └── [3,1]
    │   │   ├── [3,1]
    │   │   │   └── [2,3]
    │   │   └── [3,3]
    │   ├── [0,3]
    │   │   ├── [2,2]
    │   │   └── [3,1]
    │   ├── [2,2]
    │   │   └── [0,3]
    │   ├── [2,3]
    │   │   ├── [0,2]
    │   │   │   └── [3,1]
    │   │   └── [3,1]
    │   │       └── [0,2]
    │   ├── [3,1]
    │   │   ├── [0,2]
    │   │   │   └── [2,3]
    │   │   ├── [0,3]
    │   │   └── [2,3]
    │   │       └── [0,2]
    │   └── [3,3]
    │       └── [0,2]
    ├── [1,1]
    │   ├── [0,3]
    │   │   └── [3,2]
    │   ├── [2,3]
    │   │   └── [3,0]
    │   ├── [3,0]
    │   │   └── [2,3]
    │   └── [3,2]
    │       └── [0,3]
    ├── [1,2]
    │   ├── [0,0]
    │   │   └── [3,1]
    │   ├── [2,0]
    │   │   └── [3,3]
    │   ├── [3,1]
    │   │   └── [0,0]
    │   └── [3,3]
    │       └── [2,0]
    ├── [1,3]
    │   ├── [0,0]
    │   │   ├── [2,1]
    │   │   └── [3,2]
    │   ├── [0,1]
    │   │   ├── [2,0]
    │   │   │   └── [3,2]
    │   │   ├── [3,0]
    │   │   └── [3,2]
    │   │       └── [2,0]
    │   ├── [2,0]
    │   │   ├── [0,1]
    │   │   │   └── [3,2]
    │   │   └── [3,2]
    │   │       └── [0,1]
    │   ├── [2,1]
    │   │   └── [0,0]
    │   ├── [3,0]
    │   │   └── [0,1]
    │   └── [3,2]
    │       ├── [0,0]
    │       ├── [0,1]
    │       │   └── [2,0]
    │       └── [2,0]
    │           └── [0,1]
    ├── [2,0]
    │   ├── [0,1]
    │   │   ├── [1,3]
    │   │   │   └── [3,2]
    │   │   ├── [3,2]
    │   │   │   └── [1,3]
    │   │   └── [3,3]
    │   ├── [0,3]
    │   │   └── [3,2]
    │   ├── [1,2]
    │   │   └── [3,3]
    │   ├── [1,3]
    │   │   ├── [0,1]
    │   │   │   └── [3,2]
    │   │   └── [3,2]
    │   │       └── [0,1]
    │   ├── [3,2]
    │   │   ├── [0,1]
    │   │   │   └── [1,3]
    │   │   ├── [0,3]
    │   │   └── [1,3]
    │   │       └── [0,1]
    │   └── [3,3]
    │       ├── [0,1]
    │       └── [1,2]
    ├── [2,1]
    │   ├── [0,0]
    │   │   └── [1,3]
    │   ├── [0,2]
    │   │   └── [3,3]
    │   ├── [1,3]
    │   │   └── [0,0]
    │   └── [3,3]
    │       └── [0,2]
    ├── [2,2]
    │   ├── [0,1]
    │   │   └── [3,0]
    │   ├── [0,3]
    │   │   └── [1,0]
    │   ├── [1,0]
    │   │   └── [0,3]
    │   └── [3,0]
    │       └── [0,1]
    ├── [2,3]
    │   ├── [0,0]
    │   │   └── [3,1]
    │   ├── [0,2]
    │   │   ├── [1,0]
    │   │   │   └── [3,1]
    │   │   ├── [3,0]
    │   │   └── [3,1]
    │   │       └── [1,0]
    │   ├── [1,0]
    │   │   ├── [0,2]
    │   │   │   └── [3,1]
    │   │   └── [3,1]
    │   │       └── [0,2]
    │   ├── [1,1]
    │   │   └── [3,0]
    │   ├── [3,0]
    │   │   ├── [0,2]
    │   │   └── [1,1]
    │   └── [3,1]
    │       ├── [0,0]
    │       ├── [0,2]
    │       │   └── [1,0]
    │       └── [1,0]
    │           └── [0,2]
    ├── [3,0]
    │   ├── [0,1]
    │   │   ├── [1,3]
    │   │   └── [2,2]
    │   ├── [0,2]
    │   │   └── [2,3]
    │   ├── [1,1]
    │   │   └── [2,3]
    │   ├── [1,3]
    │   │   └── [0,1]
    │   ├── [2,2]
    │   │   └── [0,1]
    │   └── [2,3]
    │       ├── [0,2]
    │       └── [1,1]
    ├── [3,1]
    │   ├── [0,0]
    │   │   ├── [1,2]
    │   │   └── [2,3]
    │   ├── [0,2]
    │   │   ├── [1,0]
    │   │   │   └── [2,3]
    │   │   └── [2,3]
    │   │       └── [1,0]
    │   ├── [0,3]
    │   │   └── [1,0]
    │   ├── [1,0]
    │   │   ├── [0,2]
    │   │   │   └── [2,3]
    │   │   ├── [0,3]
    │   │   └── [2,3]
    │   │       └── [0,2]
    │   ├── [1,2]
    │   │   └── [0,0]
    │   └── [2,3]
    │       ├── [0,0]
    │       ├── [0,2]
    │       │   └── [1,0]
    │       └── [1,0]
    │           └── [0,2]
    ├── [3,2]
    │   ├── [0,0]
    │   │   └── [1,3]
    │   ├── [0,1]
    │   │   ├── [1,3]
    │   │   │   └── [2,0]
    │   │   └── [2,0]
    │   │       └── [1,3]
    │   ├── [0,3]
    │   │   ├── [1,1]
    │   │   └── [2,0]
    │   ├── [1,1]
    │   │   └── [0,3]
    │   ├── [1,3]
    │   │   ├── [0,0]
    │   │   ├── [0,1]
    │   │   │   └── [2,0]
    │   │   └── [2,0]
    │   │       └── [0,1]
    │   └── [2,0]
    │       ├── [0,1]
    │       │   └── [1,3]
    │       ├── [0,3]
    │       └── [1,3]
    │           └── [0,1]
    └── [3,3]
        ├── [0,1]
        │   └── [2,0]
        ├── [0,2]
        │   ├── [1,0]
        │   └── [2,1]
        ├── [1,0]
        │   └── [0,2]
        ├── [1,2]
        │   └── [2,0]
        ├── [2,0]
        │   ├── [0,1]
        │   └── [1,2]
        └── [2,1]
            └── [0,2]

Printing all possible solutions :
0 1 0 0 
0 0 0 2 
3 0 0 0 
0 0 4 0 
_______
0 1 0 0 
0 0 0 2 
4 0 0 0 
0 0 3 0 
_______
0 1 0 0 
0 0 0 3 
2 0 0 0 
0 0 4 0 
_______
0 1 0 0 
0 0 0 4 
2 0 0 0 
0 0 3 0 
_______
0 1 0 0 
0 0 0 3 
4 0 0 0 
0 0 2 0 
_______
0 1 0 0 
0 0 0 4 
3 0 0 0 
0 0 2 0 
_______
0 0 1 0 
2 0 0 0 
0 0 0 3 
0 4 0 0 
_______
0 0 1 0 
2 0 0 0 
0 0 0 4 
0 3 0 0 
_______
0 0 1 0 
3 0 0 0 
0 0 0 2 
0 4 0 0 
_______
0 0 1 0 
4 0 0 0 
0 0 0 2 
0 3 0 0 
_______
0 0 1 0 
3 0 0 0 
0 0 0 4 
0 2 0 0 
_______
0 0 1 0 
4 0 0 0 
0 0 0 3 
0 2 0 0 
_______
0 0 2 0 
1 0 0 0 
0 0 0 3 
0 4 0 0 
_______
0 0 2 0 
1 0 0 0 
0 0 0 4 
0 3 0 0 
_______
0 0 3 0 
1 0 0 0 
0 0 0 2 
0 4 0 0 
_______
0 0 4 0 
1 0 0 0 
0 0 0 2 
0 3 0 0 
_______
0 0 3 0 
1 0 0 0 
0 0 0 4 
0 2 0 0 
_______
0 0 4 0 
1 0 0 0 
0 0 0 3 
0 2 0 0 
_______
0 2 0 0 
0 0 0 1 
3 0 0 0 
0 0 4 0 
_______
0 2 0 0 
0 0 0 1 
4 0 0 0 
0 0 3 0 
_______
0 3 0 0 
0 0 0 1 
2 0 0 0 
0 0 4 0 
_______
0 4 0 0 
0 0 0 1 
2 0 0 0 
0 0 3 0 
_______
0 3 0 0 
0 0 0 1 
4 0 0 0 
0 0 2 0 
_______
0 4 0 0 
0 0 0 1 
3 0 0 0 
0 0 2 0 
_______
0 2 0 0 
0 0 0 3 
1 0 0 0 
0 0 4 0 
_______
0 2 0 0 
0 0 0 4 
1 0 0 0 
0 0 3 0 
_______
0 3 0 0 
0 0 0 2 
1 0 0 0 
0 0 4 0 
_______
0 4 0 0 
0 0 0 2 
1 0 0 0 
0 0 3 0 
_______
0 3 0 0 
0 0 0 4 
1 0 0 0 
0 0 2 0 
_______
0 4 0 0 
0 0 0 3 
1 0 0 0 
0 0 2 0 
_______
0 0 2 0 
3 0 0 0 
0 0 0 1 
0 4 0 0 
_______
0 0 2 0 
4 0 0 0 
0 0 0 1 
0 3 0 0 
_______
0 0 3 0 
2 0 0 0 
0 0 0 1 
0 4 0 0 
_______
0 0 4 0 
2 0 0 0 
0 0 0 1 
0 3 0 0 
_______
0 0 3 0 
4 0 0 0 
0 0 0 1 
0 2 0 0 
_______
0 0 4 0 
3 0 0 0 
0 0 0 1 
0 2 0 0 
_______
0 0 2 0 
3 0 0 0 
0 0 0 4 
0 1 0 0 
_______
0 0 2 0 
4 0 0 0 
0 0 0 3 
0 1 0 0 
_______
0 0 3 0 
2 0 0 0 
0 0 0 4 
0 1 0 0 
_______
0 0 4 0 
2 0 0 0 
0 0 0 3 
0 1 0 0 
_______
0 0 3 0 
4 0 0 0 
0 0 0 2 
0 1 0 0 
_______
0 0 4 0 
3 0 0 0 
0 0 0 2 
0 1 0 0 
_______
0 2 0 0 
0 0 0 3 
4 0 0 0 
0 0 1 0 
_______
0 2 0 0 
0 0 0 4 
3 0 0 0 
0 0 1 0 
_______
0 3 0 0 
0 0 0 2 
4 0 0 0 
0 0 1 0 
_______
0 4 0 0 
0 0 0 2 
3 0 0 0 
0 0 1 0 
_______
0 3 0 0 
0 0 0 4 
2 0 0 0 
0 0 1 0 
_______
0 4 0 0 
0 0 0 3 
2 0 0 0 
0 0 1 0 
_______
Number of answers : 48
___________________________________
behrad@TadavomnisT:~/Desktop$

این پرینت درخت برای یادگیری شماست ، شما برنامه بهینه تری بنویسید.

و البته سورسکد کلاسی که نوشتیم:

back_tracking.php

<?php

set_time_limit(0);

// // // // // // // // // // // // // // // // // // // // // // // // // // // 
// //                                                                      // // 
// //                              NOTICE:                                 // // 
// //                                                                      // // 
// //                  THIS IS NOT AN OPTIMISED SCRIPT!                    // // 
// //                  THIS IS NOT AN OPTIMISED SCRIPT!                    // // 
// //                  THIS IS NOT AN OPTIMISED SCRIPT!                    // // 
// //                  THIS IS NOT AN OPTIMISED SCRIPT!                    // // 
// //                                                                      // // 
// //                                                                      // // 
// //             THIS SCRIPT IS JUST FOR EDUCATIONAL PURPOSES             // // 
// //                                                                      // // 
// //               CLASSES AND FUNCTIONS BY : TadavomnisT                 // // 
// //                                                                      // // 
// //                                                                      // // 
// //                    GitHub gist for this script:                      // // 
// // https://gist.github.com/TadavomnisT/d9fc6ba06dcb775b5ee8cf8baaa94588 // // 
// //                                                                      // // 
// //                 GitHub repositpry for this script:                   // // 
// // https://github.com/TadavomnisT/My_gists/tree/main/php_back_tracking  // // 
// //                                                                      // // 
// // // // // // // // // // // // // // // // // // // // // // // // // // //

n_rooks( 4 );

n_rooks( 4 , true ); //distinguish between rooks

// // -----------------------------------------------------

n_queens( 4 );

n_queens( 4 , true ); //distinguish between queens

// =============================================================================
// =============================================================================
// FUNCTIONS====================================================================
// =============================================================================
// =============================================================================

function n_rooks( int $size , bool $distinguish = false )
{
    echo PHP_EOL . "** $size ROOKS **" . (($distinguish)? " (distinguishing between rooks)" : " (no distinguish between rooks)") . PHP_EOL . "Building empty matrix..." . PHP_EOL;
    $matrix = [];
    for ($i = 0; $i < $size; $i++) // build empty matrix
        for ($j=0; $j <$size ; $j++)
            $matrix[$i][$j] = 0;
    echo "Building decision tree..." . PHP_EOL;
    $tree = new Tree;
    $tree->createNode( "root" );
    for ($i = 0; $i < $size ; $i++) {
        foreach ($tree->getAllNodesOfDepth($i) as $KeyOfNode) {
            $tempNode = $tree->getNode( $KeyOfNode );
            $forbiddenRows = [];
            $forbiddenColumns = [];
            while (!$tempNode->isRoot()) {
                $forbiddenRows[] = $tempNode->getValue()[0]; 
                $forbiddenColumns[] = $tempNode->getValue()[1];
                $tempNode = $tree->getNode( $tempNode->getParent() );
            }
            for ($j = 0; $j < $size  ; $j++) { 
                for ($k = 0; $k < $size  ; $k++) { 
                    if ( !in_array( $j , $forbiddenRows ) && !in_array( $k , $forbiddenColumns ) ) $tree->createChild( [$j , $k] , $KeyOfNode );
                }
            }
        }
    }
    echo "Printing decision tree :" . PHP_EOL;
    $tree->printTree();
    echo PHP_EOL . "Printing all possible solutions :" . PHP_EOL;
    $printedMatrixes = [];
    $answerCounter = 0;
    if (!$distinguish) $symmetricCounter = 0;
    foreach ($tree->getAllNodesOfDepth($size) as $KeyOfNode) {
        $tempMatrix = $matrix;
        $tempNode = $tree->getNode( $KeyOfNode );
        $counter = $size;
        while (!$tempNode->isRoot()) {
            $coordinate = $tempNode->getValue(); 
            $tempMatrix[ $coordinate[0] ][ $coordinate[1] ] = ($distinguish) ? $counter : 1 ;
            $tempNode = $tree->getNode( $tempNode->getParent() );
            --$counter;
        }
        if (!$distinguish) {
            if ( !in_array( $tempMatrix , $printedMatrixes  ) ) {
                if(is_symmetric($tempMatrix , $size)){
                    echo "**symmetric**" . PHP_EOL;
                    ++$symmetricCounter;
                } 
                for ($i=0; $i < $size; $i++) { // print matrix
                    for ($j=0; $j <$size ; $j++) { 
                        echo $tempMatrix[$i][$j] . " ";
                    }
                    echo PHP_EOL;
                }
                echo str_repeat("_" , $size * 2 - 1) . PHP_EOL;
                ++ $answerCounter;
            }
            $printedMatrixes[] = $tempMatrix;
        }
        else{
            for ($i=0; $i < $size; $i++) { // print matrix
                for ($j=0; $j <$size ; $j++) { 
                    echo $tempMatrix[$i][$j] . " ";
                }
                echo PHP_EOL;
            }
            echo str_repeat("_" , $size * 2 - 1) . PHP_EOL;
            ++ $answerCounter;
        }
    }
    echo "Number of answers : " . $answerCounter . PHP_EOL;
    if (!$distinguish) echo "Number of symmetric answers : " . $symmetricCounter . PHP_EOL;
    echo "___________________________________" .PHP_EOL;
}

function n_queens( int $size , $distinguish = false )
{
    echo PHP_EOL  . "** $size QUEENS **" . (($distinguish)? " (distinguishing between queens)" : " (no distinguish between queens)") . PHP_EOL .  "Building empty matrix..." . PHP_EOL;
    $matrix = [];
    for ($i = 0; $i < $size; $i++) // build empty matrix
        for ($j=0; $j <$size ; $j++)
            $matrix[$i][$j] = 0;
    echo "Building decision tree..." . PHP_EOL;
    $tree = new Tree;
    $tree->createNode( "root" );
    for ($i = 0; $i < $size ; $i++) {
        foreach ($tree->getAllNodesOfDepth($i) as $KeyOfNode) {
            $tempNode = $tree->getNode( $KeyOfNode );
            $forbiddenRows = [];
            $forbiddenColumns = [];
            $forbiddenSums = [];
            $forbiddenSubs = [];
            while (!$tempNode->isRoot()) {
                $forbiddenRows[] = $tempNode->getValue()[0]; 
                $forbiddenColumns[] = $tempNode->getValue()[1];
                $forbiddenSums[] = $tempNode->getValue()[1] + $tempNode->getValue()[0];
                $forbiddenSubs[] = $tempNode->getValue()[1] - $tempNode->getValue()[0];
                $tempNode = $tree->getNode( $tempNode->getParent() );
            }
            for ($j = 0; $j < $size  ; $j++) { 
                for ($k = 0; $k < $size  ; $k++) { 
                    if ( !in_array( $j , $forbiddenRows ) && 
                        !in_array( $k , $forbiddenColumns) &&
                        !in_array( $k + $j , $forbiddenSums) &&
                        !in_array( $k - $j , $forbiddenSubs)
                        ){
                            $tree->createChild( [$j , $k] , $KeyOfNode );
                        }
                }
            }
        }
    }
    echo "Printing decision tree :" . PHP_EOL;
    $tree->printTree();
    echo PHP_EOL . "Printing all possible solutions :" . PHP_EOL;
    $printedMatrixes = [];
    $answerCounter = 0;
    if (!$distinguish) $symmetricCounter = 0;
    foreach ($tree->getAllNodesOfDepth($size) as $KeyOfNode) {
        $tempMatrix = $matrix;
        $tempNode = $tree->getNode( $KeyOfNode );
        $counter = $size;
        while (!$tempNode->isRoot()) {
            $coordinate = $tempNode->getValue(); 
            $tempMatrix[ $coordinate[0] ][ $coordinate[1] ] = ($distinguish) ? $counter : 1 ;
            $tempNode = $tree->getNode( $tempNode->getParent() );
            --$counter;
        }
        if (!$distinguish) {
            if ( !in_array( $tempMatrix , $printedMatrixes  ) ) {
                if(is_symmetric($tempMatrix , $size)){
                    echo "**symmetric**" . PHP_EOL;
                    ++$symmetricCounter;
                } 
                for ($i=0; $i < $size; $i++) { // print matrix
                    for ($j=0; $j <$size ; $j++) { 
                        echo $tempMatrix[$i][$j] . " ";
                    }
                    echo PHP_EOL;
                }
                echo str_repeat("_" , $size * 2 - 1) . PHP_EOL;
                ++ $answerCounter;
            }
            $printedMatrixes[] = $tempMatrix;
        }
        else{
            for ($i=0; $i < $size; $i++) { // print matrix
                for ($j=0; $j <$size ; $j++) { 
                    echo $tempMatrix[$i][$j] . " ";
                }
                echo PHP_EOL;
            }
            echo str_repeat("_" , $size * 2 - 1) . PHP_EOL;
            ++ $answerCounter;
        }
    }
    echo "Number of answers : " . $answerCounter . PHP_EOL;
    if (!$distinguish) echo "Number of symmetric answers : " . $symmetricCounter . PHP_EOL;
    echo "___________________________________" .PHP_EOL;
}

function is_symmetric( array $matrix , int $size )
{
    for ($i=0; $i < $size; $i++) 
        for ($j=0; $j <$size ; $j++) 
            if( $matrix[$i][$j] !== $matrix[$j][$i] ) return false ;
    return true;
}

function n_rooks_optimised( int $size ) //Try to directly print solutions instead of storing them in tree.
{
    # code...
}

function n_queens_optimised( int $size ) //Try to directly print solutions instead of storing them in tree.
{
    # code...
}

// =============================================================================
// =============================================================================
// CLASSES======================================================================
// =============================================================================
// =============================================================================

class Tree
{
    private $nodes = [];

    public function __construct( ) {
        #-------constructor? maybe later:))
    }
    public function setValue( int $nodeNumber , $value )
    {
        $this->nodes[$nodeNumber]->setValue($value); 
        return [
            "key" => $nodeNumber,
            "node" => $this->nodes[$nodeNumber]
        ];
    }
    public function deleteNode(int $nodeNumber) //NOT IMPLEMENTED YET
    {
        # code...
    }
    public function breadthFirst() //NOT IMPLEMENTED YET
    {
        # code...
    }
    public function depthFirst() //NOT IMPLEMENTED YET
    {
        # code...
    }
    public function getAllNodes()
    {
        return $this->nodes;
    }
    public function getAllNodesOfDepth( int $depth )
    {
        $return = [];
        foreach ($this->nodes as $key => $node) {
            if( $this->getNodeDepth( $key ) == $depth ) $return[] = $key;
        }
        return $return;
    }
    public function createNode( $value = null , int $parent = null , array $children = [])
    {
        $this->nodes[] = new Node ( $value , $parent , $children );
        return [
            "key" => (count( $this->nodes ) -1),
            "node" => $this->nodes[(count( $this->nodes ) -1)]
        ];
    }
    public function createChild(  $value = null ,  int $parent = null  )
    {
        $this->nodes[] = new Node ( $value , $parent , [] );
        $this->nodes[$parent]->addChildren( (count( $this->nodes ) -1) );
        return [
            "key" => (count( $this->nodes ) -1),
            "node" => $this->nodes[(count( $this->nodes ) -1)]
        ];
    }
    public function getChildren( $nodeNumber )
    {
        return $this->nodes[ $nodeNumber ]->getChildren;
    }
    public function getNode( $nodeNumber )
    {
        return $this->nodes[ $nodeNumber ];
    }
    public function getRoot()
    {
        foreach ($this->nodes as $key => $node) {
            if ($node->getParent() === null) return ["key" => $key , "node" => $node];
        }
        return false;
    }
    public function getTreeDepth()
    {
        if( count($this->nodes) === 0 ) return 0;
        $tempNode = $this->getRoot()['node'];
        $depth = 0;
        do {
            $tempNode= $this->nodes[$tempNode->children[0]];
            $depth++;
        }while (!($tempNode->isLeafe()));
        return $depth;
    }
    public function getNodeDepth( $nodeNumber )
    {
        if( count($this->nodes) === 0 ) return 0;
        $tempNode = $this->nodes[ $nodeNumber ];
        $depth = 0;
        while (!($tempNode->isRoot())){
            $tempNode = $this->nodes[$tempNode->getParent()];
            $depth++;
        }
        return $depth;
    }
    private function convertToArray( $processNode = NULL )
    {
        if($processNode == NULL) $processNode = $this->getRoot()['node'];
        if ( count( $processNode->getChildren() ) > 0 )
        foreach ($processNode->getChildren() as $node) {
            if ( count( $this->nodes[$node]->getChildren() ) == 0 )
            $return[ json_encode($processNode->getValue()) ][] = $this->convertToArray( $this->nodes[$node] )  ;
            else $return[ json_encode($processNode->getValue()) ] = ((isset($return)) ? $return[ json_encode($processNode->getValue()) ] : []) + $this->convertToArray( $this->nodes[$node] )  ;
        }
        else $return = json_encode($processNode->getValue());
        return $return; 
    }
    private function printArray( array $tree , string $key = "." , string $stack = "" , $first = TRUE , $firstPadding = NULL )
    {
        if ( gettype($tree) == "array" )
        {
            if($firstPadding === NULL) $firstPadding = ( count($tree)>1 ) ? "│   " : "    " ;
            echo   $key . PHP_EOL ;
            foreach ($tree as $key => $value) {
                if ($key === array_key_last($tree)){
                    echo (($first) ? "" : $firstPadding ) . $stack . "└── ";
                    $padding = "    ";
                    if($first) $firstPadding = "    ";
                }
                else {
                    echo (($first) ? "" : $firstPadding ) . $stack . "├── ";
                    $padding = "│   ";
                }
                if( is_array($value) )$this->printArray( $value , $key ,   $stack . (($first) ? "" : $padding ) , FALSE , $firstPadding );
                else echo $key . " -> " . $value . PHP_EOL;
            }
        }
        else echo $tree . PHP_EOL;
    }
    public function printTree()
    {
        if( count($this->nodes) < 1 ) echo "EMPTY TREE" . PHP_EOL;
        else if( count($this->nodes) == 1 ) echo $this->getRoot()["node"]->getValue() . PHP_EOL;
        else $this->printArray( $this->convertToArray() );
        return true;
    }
}

class Node 
{
    private $value;
    private $parent = null;
    private $children = [];

    public function __construct( $value = null , int $parent = null , array $children = []) {        
        $this->value = $value;
        $this->parent = $parent;
        $this->children = $children;
    }
    public function getValue()
    {
        return $this->value;
    }
    public function getParent()
    {
        return $this->parent;
    }
    public function getChildren()
    {
        return $this->children;
    }
    public function setValue( $newValue )
    {
        $this->value = $newValue;
        return $this->value;
    }
    public function setParent( $newParent )
    {
        $this->parent = $newParent;
        return $this->parent;
    }
    public function setChildren( $newChildren = [] )
    {
        $this->children = $newChildren;
        return $this->children;
    }
    public function addChildren( $newChild )
    {
        $this->children[] = $newChild;
        return $this->children;
    }
    public function delParent()
    {
        $this->parent = null;
        return true;
    }
    public function delChildren( $index )
    {
        unset($this->children[$index]);
        return $this->children;
    }
    public function delAllChildren()
    {
        $this->children = [];
        return $this->children;
    }
    public function isLeafe()
    {
        if( count($this->children) === 0 ) return true;
        return false;
    }
    public function isRoot()
    {
        if( $this->parent === NULL ) return true;
        return false;
    }
}

// =============================================================================
// =============================================================================
// EXAMPLES=====================================================================
// =============================================================================
// =============================================================================


// // AN EXAMPLE TO SHOW HOW TO USE TREE CLASS==================================
// $tree = new Tree;
// $root = $tree->createNode( "root" );
// $firstDepthChild1 = $tree->createChild( [1,2] , $root["key"] );
// $firstDepthChild2 = $tree->createChild( [0,1] , $root["key"] );
// $firstDepthChild3 = $tree->createChild( [1,1] , $root["key"] );
// $secondDepthChild1 = $tree->createChild( [0,0] , $firstDepthChild3["key"] );
// $secondDepthChild2 = $tree->createChild( [2,0] , $firstDepthChild3["key"] );
// $secondDepthChild3 = $tree->createChild( [3,3] , $secondDepthChild2["key"] );
// $tree->printTree();
// var_dump($tree->getAllNodesOfDepth(4));
// // ==========================================================================


?>

چجوری یه درخت رو توی PHP چاپ کنیم؟

و آخرین مطلب در محضر شما بزرگواران پاسخ تمرینی هست که دادم ، چون دلم نمیاد پاسخشو ناگفته بذارم ، گرچه توی سورس‌کد هست ولی نسخه ساده‌شو میذارم:
تمرین1 : بدون اینکه به سورسکد نگاه کنید تابعی بنویسید که یک آرایه چند بعدی رو بگیره و به شکل درخت ترمینالی (مثل کامند tree یا pstree ) ویژوآلایز کنه.

پاسخ تمرین 1 :

function printTree( array $tree , string $key = "." , string $stack = "" , $first = TRUE , $firstPadding = NULL )
{
    if ( gettype($tree) == "array" )
    {
        if($firstPadding === NULL) $firstPadding = ( count($tree)>1 ) ? "│   " : "    " ;
        echo   $key . PHP_EOL ;
        foreach ($tree as $key => $value) {
            if ($key === array_key_last($tree)){
                echo (($first) ? "" : $firstPadding ) . $stack . "└── ";
                $padding = "    ";
                if($first) $firstPadding = "    ";
            }
            else {
                echo (($first) ? "" : "$firstPadding" ) . $stack . "├── ";
                $padding = "│   ";
            }
            if( is_array($value) )printTree( $value , $key ,   $stack . (($first) ? "" : $padding ) , FALSE , $firstPadding );
            else echo $key . " -> " . $value . PHP_EOL;
        }
    }
    else echo $tree . PHP_EOL;
}

استفاده از فانکشن:

visualize_tree.php

<?php

// // // // // // // // // // // // // // // // // // // // // // // // // // // 
// //                                                                      // // 
// //                                                                      // // 
// //                    PHP print array like a Tree                       // // 
// //                                                                      // // 
// //                         Visualizing Tree                             // // 
// //                                                                      // // 
// //                     FUNCTION BY : TadavomnisT                        // // 
// //                                                                      // // 
// //                                                                      // // 
// //                    GitHub gist for this script:                      // // 
// // https://gist.github.com/TadavomnisT/f83519f3503b74663c81af5d6c68dd82 // // 
// //                                                                      // // 
// //                 GitHub repositpry for this script:                   // // 
// //   https://github.com/TadavomnisT/My_gists/tree/main/visualize_tree   // //
// //                                                                      // // 
// // // // // // // // // // // // // // // // // // // // // // // // // // //


function printTree( array $tree , string $key = "." , string $stack = "" , $first = TRUE , $firstPadding = NULL )
{
    if ( gettype($tree) == "array" )
    {
        if($firstPadding === NULL) $firstPadding = ( count($tree)>1 ) ? "│   " : "    " ;
        echo   $key . PHP_EOL ;
        foreach ($tree as $key => $value) {
            if ($key === array_key_last($tree)){
                echo (($first) ? "" : $firstPadding ) . $stack . "└── ";
                $padding = "    ";
                if($first) $firstPadding = "    ";
            }
            else {
                echo (($first) ? "" : $firstPadding ) . $stack . "├── ";
                $padding = "│   ";
            }
            if( is_array($value) )printTree( $value , $key ,   $stack . (($first) ? "" : $padding ) , FALSE , $firstPadding );
            else echo $key . " -> " . $value . PHP_EOL;
        }
    }
    else echo $tree . PHP_EOL;
}



// ---------------------------------------TESTING FUNCTION-------------------------------------


$sample_array_1 = 
[
    0 => [
        'item_id' => 6,
        'price' => "2311.00",
        'qty' => 12,
        'discount' => 0
    ],
    1 => [
        'item_id' => 7,
        'price' => "1231.00",
        'qty' => 1,
        'discount' => 12
    ],
    2 => [
        'item_id' => 8,
        'price' => "123896.00",
        'qty' => 0,
        'discount' => 24
    ]
];
$sample_array_2 = array(
    array(
         "name"=>"John",
        "lastname"=>"Doe",
        "country"=>"Japan",
        "nationality"=>"Japanese",
        "job"=>"web developer",
        "hobbies"=>array(
                "sports"=>"soccer",
                "others"=>array(
                        "freetime"=>"watching Tv"
                )
        )

    )
);
$sample_array_3 = [
    "root" => [
        "first_depth_node1" =>[
            "second_depth_node1",
            "second_depth_node2" => [
                "third_depth_node1" ,
                "third_depth_node2" ,
                "third_depth_node3" => [
                    "fourth_depth_node1",
                    "fourth_depth_node2",
                ]
                ],
            "second_depth_node3",
        ] ,
        "first_depth_node2" => [
            "second_depth_node4" => [ "third_depth_node3" => [1]]
        ]
        ]
];
$sample_array_4 = [];
$sample_array_5 = ["1"];
$sample_array_6 = [
    "T",
    "Ta",
    "Tad",
    "Tada",
    "Tadav",
    "Tadavo",
    "Tadavom",
    "Tadavomn",
    "Tadavomni",
    "Tadavomnis",
    "TadavomnisT",
];


printTree($sample_array_1);
echo PHP_EOL . "------------------------------" . PHP_EOL;
printTree($sample_array_2);
echo PHP_EOL . "------------------------------" . PHP_EOL;
printTree($sample_array_3);
echo PHP_EOL . "------------------------------" . PHP_EOL;
printTree($sample_array_4);
echo PHP_EOL . "------------------------------" . PHP_EOL;
printTree($sample_array_5);
echo PHP_EOL . "------------------------------" . PHP_EOL;
printTree($sample_array_6);


?>

نتیجه:

php visualize_tree.php

.
├── 0
│   ├── item_id -> 6
│   ├── price -> 2311.00
│   ├── qty -> 12
│   └── discount -> 0
├── 1
│   ├── item_id -> 7
│   ├── price -> 1231.00
│   ├── qty -> 1
│   └── discount -> 12
└── 2
    ├── item_id -> 8
    ├── price -> 123896.00
    ├── qty -> 0
    └── discount -> 24

------------------------------
.
└── 0
    ├── name -> John
    ├── lastname -> Doe
    ├── country -> Japan
    ├── nationality -> Japanese
    ├── job -> web developer
    └── hobbies
        ├── sports -> soccer
        └── others
            └── freetime -> watching Tv

------------------------------
.
└── root
    ├── first_depth_node1
    │   ├── 0 -> second_depth_node1
    │   ├── second_depth_node2
    │   │   ├── 0 -> third_depth_node1
    │   │   ├── 1 -> third_depth_node2
    │   │   └── third_depth_node3
    │   │       ├── 0 -> fourth_depth_node1
    │   │       └── 1 -> fourth_depth_node2
    │   └── 1 -> second_depth_node3
    └── first_depth_node2
        └── second_depth_node4
            └── third_depth_node3
                └── 0 -> 1

------------------------------
.

------------------------------
.
└── 0 -> 1

------------------------------
.
├── 0 -> T
├── 1 -> Ta
├── 2 -> Tad
├── 3 -> Tada
├── 4 -> Tadav
├── 5 -> Tadavo
├── 6 -> Tadavom
├── 7 -> Tadavomn
├── 8 -> Tadavomni
├── 9 -> Tadavomnis
└── 10 -> TadavomnisT

این کد ویژوآلایز کردن درخت، همراه با مثال و اجرای کد روی گیست گیتهاب به لینک:

https://gist.github.com/TadavomnisT/f83519f3503b74663c81af5d6c68dd82

و همچنین روی یک ریپازیتوری (اگر با لود کردن گیست مشکل داشتید ، آیپی های ایران مشکل دارن):

https://github.com/TadavomnisT/My_gists/tree/main/visualize_tree

در دسترس هستش . همچنین اگر میخواین که ویژوآلایز کردن درخت رو تحت زبانهای دیگه ای به غیر از PHP یاد بگیرید ، جمعی از دولوپرها ، یک داکیومنت عالی تهیه کردند که در لینک زیر در دسترس هست:

https://rosettacode.org/wiki/Visualize_a_tree

تا این لحظه به 46 زبان برنامه‌نویسی بهش پاسخ دادن که کد من هم بعنوان سمپل PHP بینشون هست، مابقی زبانها:

• 1 11l 
• 2 Ada 
• 3 ALGOL 68 
• 4 AppleScript 
• 5 Batch File 
• 6 BBC BASIC 
• 7 C 
• 8 C++ 
• 9 C# 
• 10 Clojure 
• 11 Common Lisp 
• 12 D 
• 13 Elena 
• 14 Erlang 
• 15 F# 
• 16 Factor 
• 17 Fōrmulæ 
• 18 Go 
• 18.1 JSON 
• 18.2 TOML 
• 18.3 Unicode 
• 19 Haskell 
• 20 Icon and Unicon 
• 21 J 
• 22 Java 
• 23 JavaScript 
• 23.1 HTML 
• 23.2 Plain text 
• 23.2.1 Vertically centered tree 
• 23.2.2 Decorated outline 
• 24 Julia 
• 25 Kotlin 
• 26 Lingo 
• 27 Maple 
• 28 Mathematica 
• 28.1 Tree graph 
• 28.2 Opener view 
• 29 Maxima 
• 30 Nim 
• 31 Perl 
• 32 Phix 
• 33 PicoLisp 
• 34 Prolog 
• 34.1 XPCE 
• 35 Python 
• 35.1 Library module 
• 35.2 Functional composition 
• 35.2.1 Vertically centered parents 
• 35.2.2 Simple decorated-outline tree 
• 36 Racket 
• 37 Raku 
• 38 REXX 
• 39 Ruby 
• 40 Rust 
• 41 Sidef 
• 42 Tcl 
• 43 Wren 
• 44 Yabasic 
• 45 zkl 
• 46 PHP

و... تموم.

لینک گیست مربوط به فایل بک ترکینگ به همراه نحوه اجرای کد:
https://gist.github.com/TadavomnisT/d9fc6ba06dcb775b5ee8cf8baaa94588

کارهای آینده

شما میتونین بک‌ترکینگ رو توی زبانهای دیگه/مسائل دیگه پیاده‌سازی کنین. برای کارهای آینده ‌ای که راجع به این مقاله میشه انجام داد میتونیم به این مورد اشاره کنیم که کد رو جوری بنویسین که درخت رو توی رم ذخیره نکنه.

کپی رایت

این یک مقاله آزاد و متن‌باز تحت مجوز GFDL1-3 می‌باشد، بنابراین اجازه کپی، توزیع و/یا تغییر این سند با شرایط مجوز GNU Free Documentation License داده شده است.

نویسنده

بهراد.ب (behroora@yahoo.com)

منابع

مسائل مرتبط با این مقاله

این مقاله بصورت آزاد و اپن‌سورس در مخزن کتابها/مقالات آزاد در لینک زیر در دسترس است:

الگوریتم بک‌ترکینگ در هوش مصنوعی 🔥

نسخه انگلیسی این مقاله:

Backtracking Algorithm in Artificial Intelligence 🔥
- The n-Queens and n-Rooks Problem
- What is the Backtracking Algorithm?

هر نوع اشکال علمی، مساله یا بحث مربوط با این مقاله را میتوانید از طریق Issue در ریپازیتوری یا ایمیل مطرح نمایید:

https://github.com/TadavomnisT/Free_Books-Documents/issues
behroora@yahoo.com